Das Dusk-Netzwerk ist mehr als nur eine weitere Privatsphäre-Münze. Es ist ein bewusster Versuch, eine Blockchain zu schaffen, auf der reale finanzielle Transaktionen stattfinden können, ohne zu offenbaren, wer was an wen und warum sendet. Um dies zu erreichen, verlässt sich das Netzwerk sehr stark auf eine kurze Liste sehr spezifischer kryptografischer Primitive: Pedersen-Verpflichtungen, Bulletproofs, EdDSA, bLSAG, BLS-Signaturen und im Allgemeinen Null-Wissen-Nachweise.
Diese wurden nicht ausgewählt, weil sie in Mode sind. Sie wurden ausgewählt, weil jede einzelne ein spezifisches Problem anspricht, das mit einfacheren Werkzeugen (grundlegendes ECDSA, grundlegende Hashes, grundlegende öffentliche Schlüssel) nicht gelöst werden kann, ohne entweder die Privatsphäre oder die Leistung zu beeinträchtigen.
Ich kann Sie durch jede Komponente führen und das tatsächliche Bedürfnis erklären, das ihre Schaffung vorangetrieben hat und wie sie alle zusammen in Dusk's Design funktionieren.
1. Pedersen-Verpflichtungen – Werte verstecken, während sie immer noch beweisen, dass sie sich summieren
Angenommen, Sie möchten Gelder on-chain senden, möchten aber nicht, dass der Betrag sichtbar ist. Das Netzwerk muss jedoch immer noch überprüfen können, dass der gesamte Betrag, der hineingeht, gleich dem gesamten Betrag ist, der hinausgeht (keine Inflation, keine magische Geldschöpfung).
Ein einfaches öffentliches Schlüsselverschlüsselungsverfahren würde es Ihnen ermöglichen, den Betrag zu verbergen. Allerdings könnten Sie dann nie beweisen, dass die beiden versteckten Beträge sich zu etwas summieren.
Pedersen-Verpflichtungen lösen dieses Problem exakt.
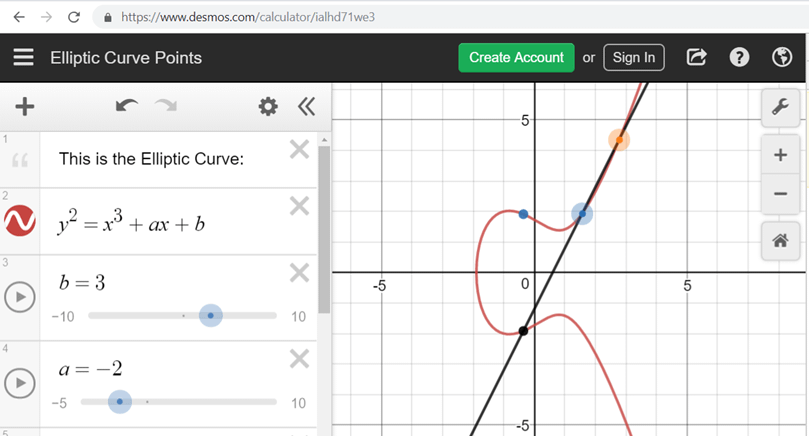
Sie wählen zwei Gruppenelemente G und H, wobei die diskrete Logarithmusbeziehung zwischen H und G unbekannt ist (in der Praxis wird H aus G über einen Hash-to-Point berechnet, sodass niemand das Logarithmus kennt). Um sich zu einem Wert x zu verpflichten, berechnen Sie C = rG + xH.
Die "Magie" hier ist:
- Diese wurden nicht ausgewählt, weil sie modisch sind. Sie wurden ausgewählt, weil jede einzelne ein spezifisches Problem anspricht, das nicht mit einfacheren Werkzeugen (grundlegende ECDSA, grundlegende Hashes, grundlegende öffentliche Schlüssel) gelöst werden kann, ohne entweder die Privatsphäre oder die Leistung zu beeinträchtigen.
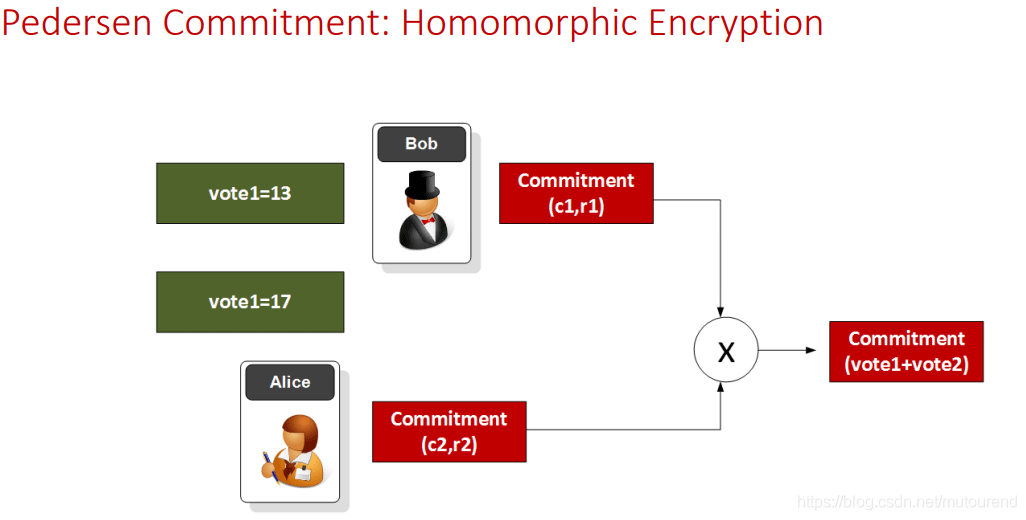
In Dusk wird dies für jede vertrauliche Transaktionsausgabe verwendet. Der Absender verpflichtet sich zu dem Betrag, den er sendet, und dem Betrag, den er erhält (das Wechselgeld). Das Netzwerk sieht nur Verpflichtungen, aber es kann beweisen, dass sie sich auf null summieren, indem es die Homomorphie verwendet. Keine Beträge gehen jemals klar in die Kette.
Vektor-Pedersen wendet dasselbe Konzept auf mehrere Werte gleichzeitig an (Betrag + Verblindung + Memo-Feld + alles andere, was Sie zusammen verbergen möchten). Deshalb präsentiert das Papier die Vektorform – Dusk muss häufig gleichzeitig mehrere Skalare verpflichten.
2. Bulletproofs – Beweis, dass "diese versteckte Zahl zwischen 0 und 2⁶⁴" liegt, ohne sie offen zu legen
Mit versteckten Zahlen kommt die nächste Herausforderung: Wie kann man beweisen, dass die Zahl nicht negativ ist (oder innerhalb eines gültigen Bereichs liegt), ohne die Zahl selbst offenzulegen?
Traditionelle Bereichsnachweise (wie in alten vertraulichen Transaktionen in Monero vor Bulletproofs) waren massiv – mehrere Kilobyte pro Ausgabe.
Bulletproofs reduzierten dies auf ~2 KB für einen 64-Bit-Bereich und wichtig ist, dass ohne vertrauenswürdige Einrichtung.
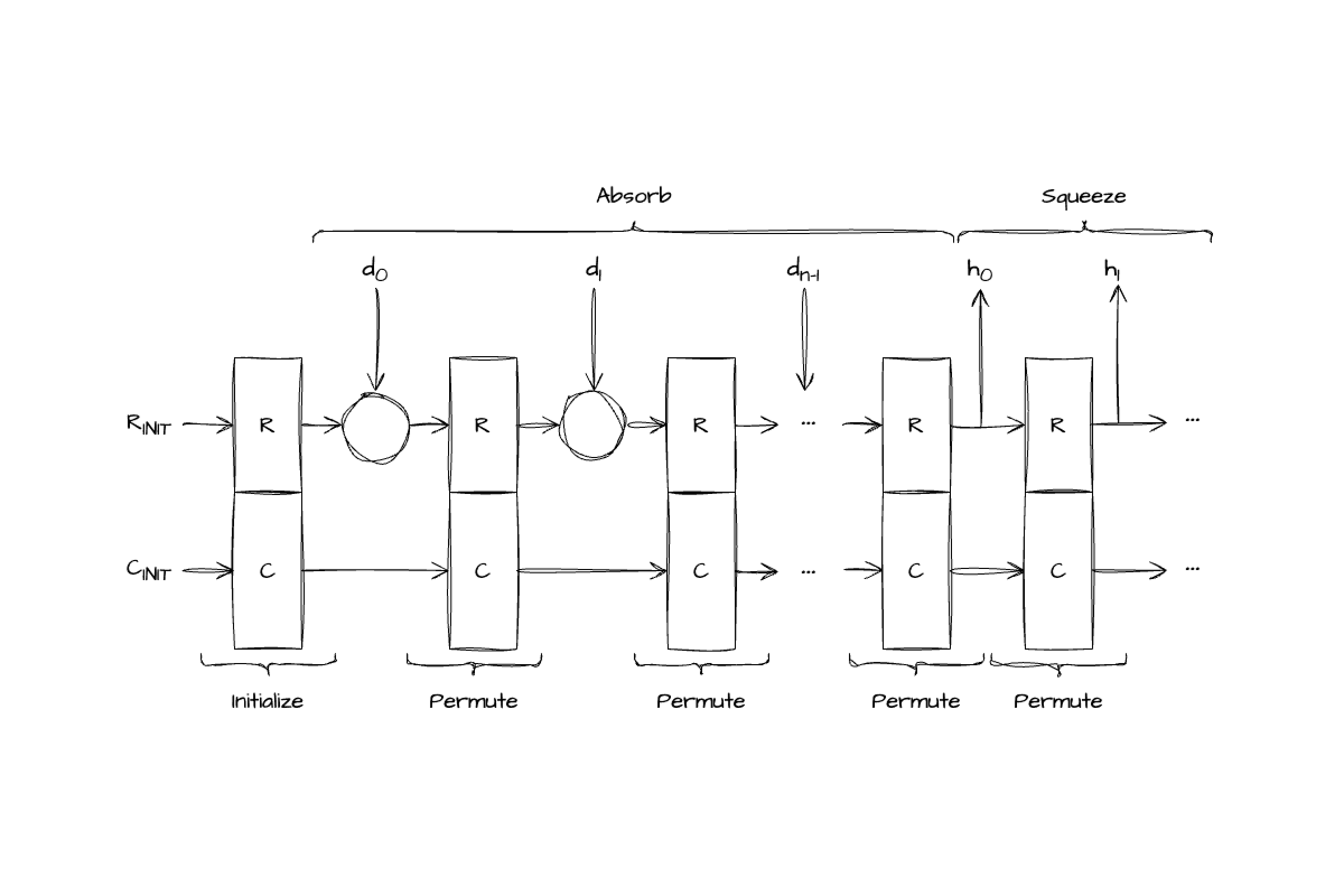
Der Schlüssel zur Effizienz von Bulletproofs ist, dass sie Behauptungen über arithmetische Schaltkreise mithilfe von Innenproduktnachweisen beweisen. Der Beweiser und der Überprüfer arbeiten beide mit Vektoren, deren Innenprodukt die Bereichseinschränkung darstellt. Die Größe des Nachweises ist lediglich logarithmisch in der Bitgröße des Bereichs.
In Dusk werden Bulletproofs verwendet, um zu beweisen:
Die Transaktionsbeträge liegen in [0, 2⁶⁴)
Korrekte Berechnung des Poseidon-Hashes (verwendet für Notenverpflichtungen) in einem Schaltkreis
Verschiedene andere kleine Integritätsprüfungen des Schaltkreises
Poseidon wurde speziell wegen seiner Eignung für arithmetische Schaltkreise (geringe multiplikative Tiefe) ausgewählt, was den Bulletproof-Schaltkreis klein und effizient zu beweisen/überprüfen hält.
Die Verifizierungszeit ist linear in der Größe des Schaltkreises, aber da die Schaltkreise, die Dusk verwendet, sehr klein sind (hauptsächlich Poseidon-Aufrufe), bleibt dies auch auf mobiler Hardware machbar.
3. Signaturschemata – die verschiedenen Rollen, die sie in Dusk spielen
Das Dusk Network ist mehr als nur eine weitere Datenschutzmünze. Es ist ein bewusster Versuch, eine Blockchain zu schaffen, auf der echte finanzielle Transaktionen stattfinden können, ohne zu offenbaren, wer was an wen und warum sendet. Um dies zu erreichen, verlässt sich das Netzwerk sehr stark auf eine Auswahl von sehr spezifischen kryptografischen Primitiven: Pedersen-Verpflichtungen, Bulletproofs, EdDSA, bLSAG, BLS-Signaturen und im Allgemeinen Null-Wissen-Beweise.
Für reguläre Peer-to-Peer-Nachrichten (Gossiping, Blockankündigungen usw.) verwendet Dusk EdDSA auf Curve25519.
Warum nicht ECDSA?
EdDSA ist deterministisch → keine schlechte Zufälligkeit kann den privaten Schlüssel offenbaren.
Die verdrehte Edwards-Kurve bietet schnellere Arithmetik und vollständige Additionsgesetze (keine Sonderfälle).
Die Signatur besteht aus lediglich zwei Gruppenelementen – sehr kompakt und effizient zu überprüfen.
Es ist das bevorzugte Schema für alles, was keine Anonymität erfordert.
bLSAG (Back Linkable Spontaneous Anonymous Group signatures) – anonymes Ausgeben mit Doppel-Ausgabe-Schutz
Dies ist die Ring-Signatur-Variante, die für das Ausgeben von Scheinen verwendet wird.
Sie haben eine Menge öffentlicher Schlüssel (den Ring). Sie beweisen, dass Sie den geheimen Schlüssel für einen von ihnen kennen, ohne zu verraten, welcher es ist. Die Größe der Signatur ist konstant, unabhängig von der Größe des Rings.
Die Verknüpfbarkeit wird durch das Schlüsselbild bereitgestellt: ein deterministischer Wert, der aus dem geheimen Schlüssel berechnet wird, und Schlüsselbilder sind einzigartig für jeden Schlüssel. Wenn Sie versuchen, denselben Schein zweimal auszugeben, stimmen die Schlüsselbilder überein → Doppel-Ausgabe erkannt.
Die "spontane" Komponente zeigt an, dass es keinen Einrichtungsprozess gibt und jeder jederzeit jeden Ring wählen kann. Die "Back"-Komponente bezieht sich auf Adam Backs Lösung, die Verknüpfbarkeit ohne Kompromittierung der Anonymität ermöglicht.
Das ist es, was Dusk ermöglicht, anonyme Transaktionen wie Monero zu haben, aber auch die Erkennung von Doppel-Ausgaben on-chain erlaubt.
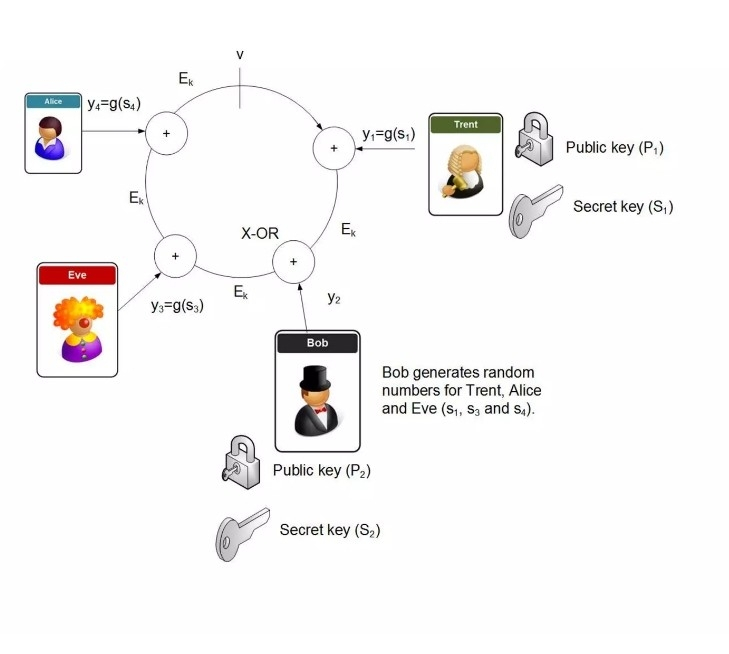
BLS-Signaturen – Aggregation für Konsens
BLS (Boneh-Lynn-Shacham) Signaturen leben auf paarungsfreundlichen Kurven (BN-254 oder BLS12-381). Die Paarung ermöglicht die Aggregation vieler Signaturen in eine kurze Signatur, die gegen den aggregierten öffentlichen Schlüssel verifiziert.
In $DUSK wird dies in der Konsensschicht angewendet: Hunderte von Validierern können denselben Block signieren, und ihre Signaturen werden on-the-fly aggregiert, sodass nur eine Signatur on-chain übrig bleibt. Die Blockgröße bleibt klein, selbst bei Tausenden von Unterzeichnern.
Der Nachteil ist, dass BLS-Signaturen eine vertrauenswürdige Einrichtung für die Kurvenparameter (oder MPC-Zeremonie) benötigen, aber danach ist es sehr leistungsfähig.
4. Null-Wissen-Nachweise – die allgemeine Philosophie
Alle oben genannten Bausteine werden letztendlich innerhalb größerer Null-Wissen-Nachweise eingesetzt.
Die Null-Wissen-Nachweise von $DUSK müssen drei Eigenschaften erfüllen (die im Papier ausdrücklich angegeben sind):
Vollständigkeit – ehrlicher Beweiser überzeugt immer ehrlichen Überprüfer.
Solidität – betrügerischer Beweiser kann den Überprüfer nur mit vernachlässigbarer Wahrscheinlichkeit überzeugen.
Null-Wissen – der Überprüfer erfährt nichts über die Wahrheit der Aussage hinaus.
Die Erklärung, warum diese drei Eigenschaften absolut unerlässlich sind, ist einfach: In einer Privatsphäre-Münze ist der Nachweis buchstäblich das einzige, was zwischen der finanziellen Privatsphäre des Benutzers und vollständiger Transparenz steht. Wenn die Solidität gebrochen ist, kann jemand gefälschtes Geld drucken. Wenn Null-Wissen gebrochen ist, ist der gesamte Punkt der Privatsphäre obsolet.
Dusk verwendet eine Mischung aus Bulletproofs (für Bereichs- und Schaltkreisnachweise) und anderen SNARK-freundlichen Methoden innerhalb seiner Transaktionsnachweise. Das bedeutet, dass der Beobachter nur den Nachweis und die Verpflichtungen sehen kann, während alles andere verborgen bleibt.

Warum dieses spezielle Set von Werkzeugen?
Es ist nicht möglich, alles mit einem einzigen Primitive zu erledigen. Pedersens gibt Ihnen Anonymität + Bindung + Additivität. Bulletproofs geben Ihnen effiziente Bereichs- und Schaltkreisnachweise zusätzlich zu diesen Verpflichtungen. bLSAG gibt Ihnen Anonymität beim Ausgeben. BLS gibt Ihnen effizienten Konsens. EdDSA gibt Ihnen schnelles alltägliches Signieren. Sie kombinieren sich alle zu einem gestuften System, in dem jede Schicht genau das Problem löst, das die Schicht darüber nicht lösen kann.
Deshalb erscheint das Design von Dusk im Vergleich zu anderen, einfacheren Ketten "über-engineered" – weil es ein schwierigerer Satz von Problemen zu lösen ist. Die meisten anderen Ketten müssen entweder Privatsphäre oder Skalierbarkeit aufgeben. Dusk versucht, beides zu bewahren, und das erfordert die Verwendung dieses speziellen Sets von kryptografischen Werkzeugen.