When I first tried to grasp how zero knowledge (ZK) algorithms work in blockchains, Dusk Network's implementation provided a clear example through its Rusk protocol. ZK algorithms allow proving knowledge of a fact without revealing the fact itself, and in Dusk, this is core to enabling private yet verifiable financial transactions. Rusk, as Dusk's state transition function, leverages ZK to process contract logic confidentially, making it a practical case study for ZK's core processes.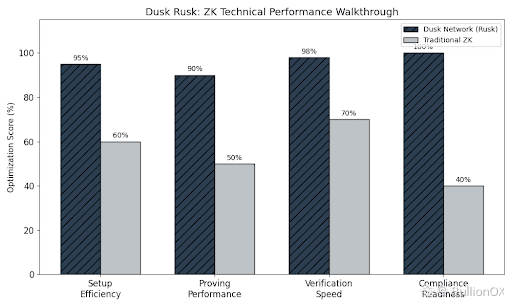
The first process is setup: ZK algorithms like PLONK (used in Dusk) start with a trusted setup phase to generate parameters for proofs. Rusk optimizes this for efficiency, creating circuits that describe contract rules in a ZK friendly way. This setup ensures proofs are succinct, allowing validators to check validity quickly without heavy computation.
Next comes proving: The prover (e.g., a user submitting a transaction) computes a proof that the state transition follows the rules. In Rusk, this happens for confidential smart contracts inputs like balances are hidden, but Rusk generates a proof showing the output is correct. The process involves polynomial commitments, where the prover commits to values and opens them selectively, containing verification to specific claims.
Verification is the final step: The verifier checks the proof against public parameters. Rusk makes this lightweight, with proofs sized in hundreds of bytes, enabling fast network consensus. For Dusk's institutional focus, this means regulators can verify compliance (e.g., limits met) without seeing data, balancing privacy with accountability.
Rusk's ZK integration supports Dusk's vision: modular execution where privacy is default but verifiable. The $DUSK token, as the economic layer, covers gas for ZK computations, aligning incentives with secure processes.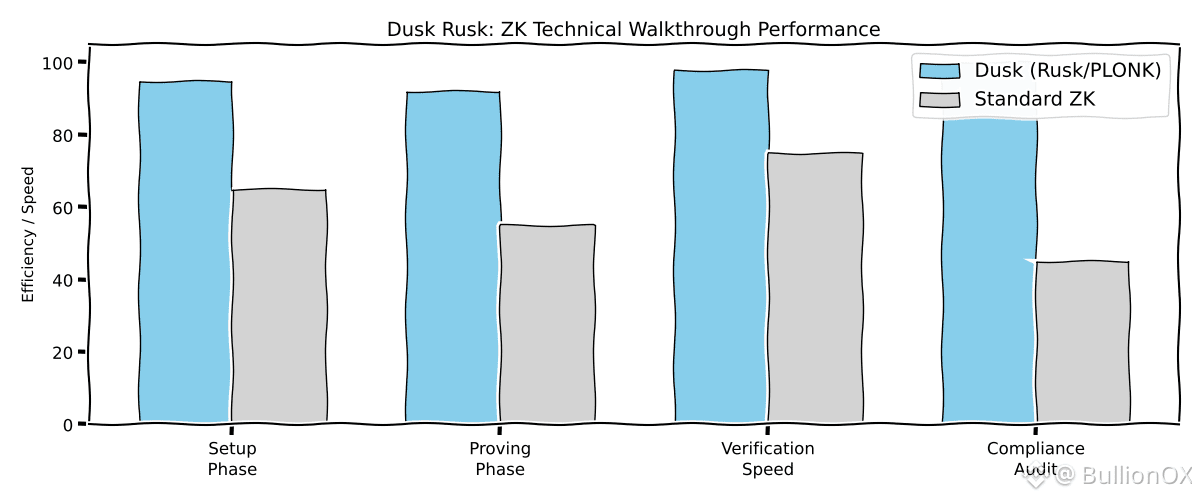
From my view, Rusk's ZK walkthrough shows how algorithms like PLONK turn privacy into a tool for trust in finance, not obscurity.
How have ZK proofs changed your blockchain projects?
What core process do you find most challenging?