#RumorsVSTruth
#ProbabilityCalculations
#IntroductionToResilientMathematics
C'è sempre quel momento, in pieno mercato crypto, in cui qualcuno dice con molta sicurezza :
« Vedrai, SOL va a 9, è scritto. »
E a volte, la versione “soft” arriva in più :
« E 90 anche, è nel mirino. »
Al momento (all'inizio 😅) della scrittura di questo articolo, SOL si aggirava intorno a 135 USDC.
Il nostro cervello vede quindi tre numeri: 135, 90, 9… e immagina una scala: 135 → 120 → 100 → 90 → 60 → 30 → 9.
Il problema è che i mercati non funzionano in “scala aritmetica” (si tolgono X dollari), ma in modo moltiplicativo (si moltiplica per 0,7, 0,5, 0,1…).
La matematica, invece, si occupa di logaritmi e probabilità.
Obiettivo di questo articolo:
1. Dimostra perché 90 e 9 non hanno nulla a che fare tra loro in termini di probabilità.
2. Stimare quanto tempo occorre affinché ciascuno di questi livelli abbia una probabilità superiore al 50% di essere raggiunto, in un modello ragionevole.
3. Paragoniamo questo al lancio di una moneta per riformulare l'intuizione.
4. Integrare:
l'indice della paura e dell'avidità,
Il DoM multivaluta (USDC, EUR, ecc.).
5. Concludere con una lettura resiliente di SOL attraverso diversi orizzonti temporali.
1. Prima insidia: il nostro cervello è lineare, il mercato no
Iniziamo con un prezzo di riferimento:
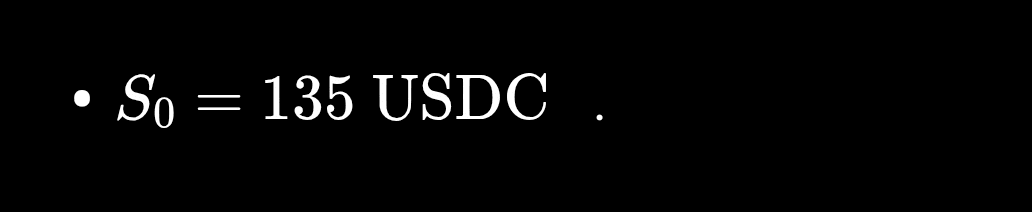
Nella discussione vengono affrontati due obiettivi:

In percentuale:
135 → 90: diminuzione di circa il 33%.
135 → 9: diminuzione di circa il 93%.
Il nostro intuito ci dice qualcosa del genere:
“90 è la versione grave, 9 è la versione estrema della stessa storia.”
Solo che in finanza non ragioniamo in termini di "+ o − X dollari", ma in termini di rapporti.
Consideriamo il logaritmo del prezzo, perché le variazioni percentuali si sommano in logaritmi.

Conclusione immediata:
Nello “spazio logaritmico”, 9 è circa 2,708 / 0,405 ≈ 6,7 volte più lontano di 90.
9 non è “un gradino sotto 90”, è un altro continente.
E come vedremo, il tempo tipico per raggiungere una certa distanza in una camminata casuale è proporzionale a d^2.
Pertanto, per una data volatilità, l'orizzonte temporale per raggiungere 9 è approssimativamente:
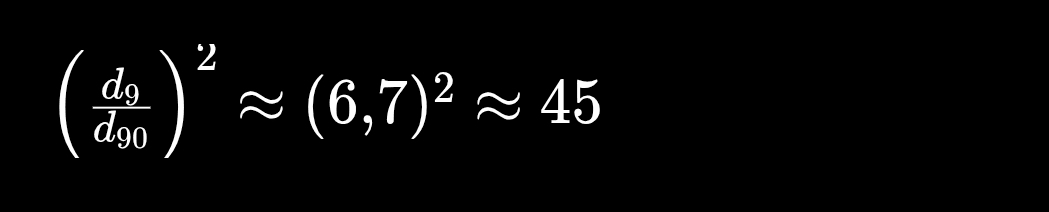
→ circa 45 volte più lungo rispetto a raggiungere 90.
2. Il framework: volatilità realistica e random walk
Adottiamo un modello semplice ma standard nella finanza.


(vale a dire, una volatilità annualizzata del 60-80%), il che è realistico per un L1 nervoso nel settore delle criptovalute.
3. Formula di base: probabilità di raggiungere un livello prima di T

dove Φ è la funzione di distribuzione cumulativa della distribuzione normale standard.
In parole:

Sappiamo che:

Questa è la formula chiave che useremo per confrontare 90 e 9.
4. 90 vs 9: orizzonti temporali tipici
Promemoria :

4.1. Tempo tipico per raggiungere 90:
Per il tempo T50(L), cioè l'orizzonte per il quale la probabilità di raggiungere il livello L è del 50%, si utilizza la seguente formula generale:
T50(L) ≈ [ d(L) / (0,674 × σ) ]²
O :
d(L) = ln(S0 / L) è la distanza in logaritmo,
σ è la volatilità annualizzata (qui tra 0,6 e 0,8),
0,674 è una costante che deriva dalla distribuzione normale (quantile del 75%).
Per il livello L = 90, con S0 = 135:
d(90) = ln(135 / 90) ≈ ln(1,5) ≈ 0,405.
Calcoliamo T50(90) per due valori di σ.
1. Si σ = 0,6 :
0,674 × 0,6 ≈ 0,404
d(90) / (0,674 × σ) ≈ 0,405 / 0,404 ≈ 1,002
T50(90) ≈ (1,002)² ≈ 1,0 un
2. Si σ = 0,8 :
0,674 × 0,8 ≈ 0,539
d(90) / (0,674 × σ) ≈ 0,405 / 0,539 ≈ 0,75
T50(90) ≈ (0,75)² ≈ 0,56 un
Conclusione pratica:
T50(90) è approssimativamente compreso tra 0,6 e 1,0 anni.
In altre parole, in un mercato neutrale ma volatile, vedere SOL raggiungere 90 almeno una volta all'anno è statisticamente abbastanza plausibile (probabilità superiore al 50%).
4.2. Tempo tipico per raggiungere 9: T50(9)
Applichiamo esattamente la stessa formula a L = 9.
Con S_0 = 135, abbiamo:
d(9) = ln(135 / 9) = ln(15) ≈ 2.708.
Calcoliamo T50(9) per gli stessi valori di σ.
1. Si σ = 0,6 :
0,674 × 0,6 ≈ 0,404
d(9) / (0,674 × σ) ≈ 2,708 / 0,404 ≈ 6,71
T50(9) ≈ (6.71)² ≈ 44.8 anni
2. Si σ = 0,8 :
0,674 × 0,8 ≈ 0,539
d(9) / (0,674 × σ) ≈ 2,708 / 0,539 ≈ 5,02
T50(9) ≈ (5.02)² ≈ 25.2 anni
Conclusione pratica:
T50(9) ha un'età compresa tra circa 25 e 45 anni.
In altre parole, nello stesso modello neutrale con volatilità realistica, ci vorrebbero diversi decenni affinché "SOL ≤ 9 almeno una volta" abbia una probabilità del 50%. Si tratta di uno scenario estremo, ben lontano da un "obiettivo naturale" nel breve o medio termine.
Inoltre, non abbiamo preso in considerazione un possibile trend rialzista a lungo termine (adozione, ricavi della rete...), il che renderebbe il 9 ancora meno probabile.
5. Probabilità su orizzonti temporali fissi (1 anno, 5 anni)
Con la formula:
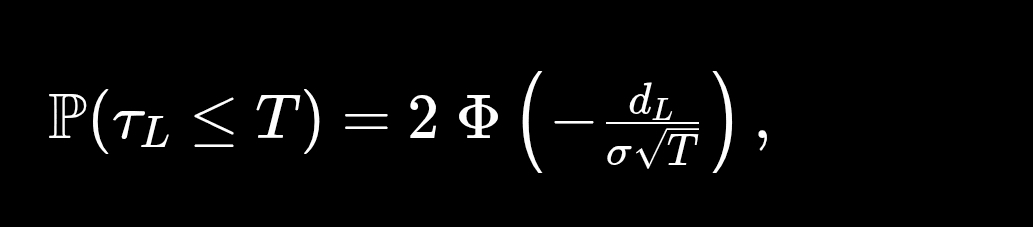
Possiamo anche fornire ordini di grandezza per un orizzonte fisso (ad esempio 1 anno, 5 anni).
Prendiamo ad esempio una volatilità intermedia:

COSÌ :
In un anno, 90 è uno scenario quasi da "lancio di moneta" (poco più del 50%),
mentre 9 è nell'ordine dello 0,01%, vale a dire un vero e proprio evento di coda della distribuzione.
Dopo 5 anni, il 90 diventa molto probabile (circa l'80%).
9 rimane in gran parte una minoranza (~8%).
6. Confronto del lancio della moneta
Per calibrare la nostra intuizione, la confrontiamo con un semplice esperimento: una moneta in equilibrio.
Probabilità di ottenere almeno una testa in n lanci:

L'analogia:
“Vedere SOL raggiungere quota 90 in un anno, in un mercato volatile”
→ Questo è un evento comune, come ottenere "almeno una Testa" in pochi lanci.
“Vedi SOL raggiungere 9 in un anno, nello stesso modello”
→ Questo è al livello di una serie molto improbabile di pile consecutive (come 12-13 di fila).
COSÌ :
Dire "SOL va a 9" perché hai appena subito un grande leg drop è un po' come dire "Sono sicuro che farò 13 stack di fila" perché hai appena perso tre lanci.
Umano... ma molto lontano da ciò che dicono le probabilità.
7. Dove collochiamo l'indice della paura e dell'avidità?
L'indice Fear & Greed misura il sentiment del mercato su una scala da 0 a 100:
0–25: paura estrema,
25–50: paura,
50–75: neutralità / ottimismo moderato,
75–100: avidità estrema.
Si calcola da:
volatilità recente,
volumi e flussi di ordini,
Dominanza di BTC,
Ricerche su Google,
attività sui social media, ecc.
È quindi strettamente legato, concettualmente, al nostro σ: più forte è la paura, più elevata tende ad essere la volatilità osservata.
Possiamo ragionare in termini di regimi:
1. Regime “normale” (indice compreso tra 30 e 70)
→ volatilità in un intervallo del 60-80% per SOL.
→ Questo è il metodo utilizzato per i nostri calcoli principali:
90 plausibili entro l'anno,
9 ultra rare.
2. Regime di paura estrema prolungato (indice persistentemente a 25)
→ volatilità effettiva che può raggiungere il 100-150%.
→ le code della distribuzione (movimenti estremi) sono più spesse.
Per esempio:

la probabilità di puntare a 9 in 1 anno aumenterebbe (saremmo fuori dallo 0,01%), ma rimarremmo molto lontani da uno scenario centrale.
In sintesi:
Sì, periodi prolungati di paura comprimono il tempo necessario per raggiungere livelli bassi.
No, non sono sufficienti a trasformare il 9 in una “destinazione naturale” nel breve termine.
Il cervello coglie lo spunto della paura e si proietta in modalità disastrosa (anche il mio spesso ci casca 🧠😅).
La matematica considera l'intera distribuzione e l'orizzonte.
8. DoM in USDC, DoM in EUR: recuperare i comportamenti
Confrontando il DoM in euro e USDC (ho piazzato un ordine da 100 € 😉) abbiamo informazioni rilevanti (sono sicuro che il tuo subconscio lo abbia già intuito, vero? 🤩
Ogni coppia ha il suo “universo psicologico”:
SOL/USDC → benchmark in dollari (100, 90, 80…).
SOL/EUR → benchmark in euro (100 €, 80 €…).
SOL/BTC → benchmark in frazioni di BTC, ecc.
In ogni order book, i trader costruiscono muri di ordini (bid/ask) attorno a questi indicatori.
Ma tutti questi mercati sono collegati dall'arbitraggio:
se SOL/EUR è “troppo basso” rispetto a SOL/USDC (una volta preso in considerazione il tasso EUR/USD),
I bot acquisteranno in EUR e venderanno in USDC e viceversa.
Ciò crea un recupero permanente in cui gli errori e le discrepanze locali vengono corretti e quindi le grandi zone di liquidità (€100, $90-95, 0,00X BTC...) alla fine si allineano.
Attraversare il DoM in più valute consente quindi: di individuare i passaggi globali del mercato, di vedere dove sono realmente concentrati gli ordini su scala globale, di non farsi ipnotizzare da un singolo numero (ad esempio solo “9”).
In un approccio resiliente, adoriamo questo: cerchiamo strutture che rimangano visibili anche quando cambiamo valuta, scala o punto di vista.
9. Lettura resiliente del SOL: breve, medio, lungo termine
Infine, applichiamo la nostra intuizione della matematica resiliente.
Idea semplificata di un “derivato resiliente” su una scala temporale:

→ Ciò si traduce in una crescita robusta a questa scala.
Senza addentrarci in una formula più sofisticata, la utilizziamo come griglia di lettura qualitativa.
9.1. A breve termine (da pochi giorni a poche settimane)
A questa scala:
Il derivato resiliente è molto volatile.
Un brusco calo lo rende improvvisamente negativo.
Un rimbalzo tecnico può riportarlo su piuttosto rapidamente.
Gli scenari rilevanti sono:
intervalli legati alla struttura della liquidità (ad esempio 135–145),
micro-tendenze guidate dalle pareti del portafoglio ordini.
A questo livello di ingrandimento, porre la domanda "9 o 90?" non ha alcun senso.
Ci occupiamo di gestione del rumore, supporto/resistenza e liquidazioni.
9.2. Medio termine (da 6 a 18 mesi)
Ecco la derivata resiliente:
attenua parte del rumore.
incorpora i cicli di paura/avidità,
inizia a riflettere l'effettiva adozione dell'ecosistema.
In questo contesto, per Solana:
Raggiungere i 90 in un ciclo di volatilità è statisticamente normale (abbiamo appena visto che è del 50-60% in un anno in un modello neutrale).
La visita 9 rimane uno scenario di coda di distribuzione, associato a:
un crollo della fiducia,
una regolamentazione o uno scandalo importante,
un problema strutturale.
Senza grandi sorprese, la matematica ci dice che nell'arco di 6-18 mesi:
90 appartiene alla parte “viva” della distribuzione,
9 rimane bloccato nella coda estrema.
9.3. A lungo termine (diversi anni)
Nel lungo termine, il derivato resiliente considera:
Il posto di Solana nell'ecosistema (DeFi, NFT, giochi, RWA…),
stabilità tecnica,
concorrenza da altre classi L1/L2
ricavi di rete, ecc.
Due scenari principali:
1. Scenario resiliente-rialzista
Solana mantiene un ruolo importante.
→ pendenza resiliente positiva a 3–5 anni,
→ 9 diventa un livello “storico” piuttosto che un obiettivo,
→ Sono ancora possibili dei cali, ma un ritorno duraturo a 9 sarebbe legato a un evento eccezionale.
2. Scenario strutturalmente ribassista
Solana risponde al telefono.
→ pendenza resiliente negativa a lungo termine,
→ Livelli molto bassi (di cui 9) diventano nuovamente accessibili nel lunghissimo termine,
→ ma in una “storia diversa” di Solana rispetto a quella che conosciamo oggi.
La matematica non prevede quale scenario si verificherà. 😭
Dicono: “ecco il posto di ogni scenario nella distribuzione delle possibilità”.
10. Conclusione: cosa corregge la matematica nella nostra intuizione
Riunendo:
il modello di volatilità,
il confronto delle distanze del registro (90 vs 9),
gli orizzonti,
l'effetto dell'indice paura/avidità,
il DOM multivaluta,
e una lettura resiliente e multiscala,
Arriviamo ad una conclusione chiara:
1. 90 e 9 non sono due “livelli” sulla stessa scala.
In termini di prezzo logaritmico, 9 è 6,7 volte più lontano di 90 e circa 45 volte più lontano in termini di tempo tipico.
2. Oltre 6-12 mesi,
90 è plausibile,
9 è praticamente impossibile in un modello di volatilità realistico senza uno shock importante.
3. Oltre 5 anni,
Il 90 diventa quasi certo (l'80% nel nostro esempio).
9 rimane un evento di minoranza (~8%).
4. L'indice paura/avidità spiega perché le menti tendono a precipitare, ma non invalida la statistica.
La paura è un regime, non una profezia.
5. Incrociando i DoM di diverse valute si scoprono le vere aree di consenso globale, anziché limitarsi a un dato isolato.
6. L'approccio resiliente colloca ogni scenario al suo posto in base all'orizzonte (breve, medio, lungo termine).
Di fronte al "furbetto" che afferma:
"SOL si sta dirigendo verso 9."
Possiamo rispondere con calma:
"Con una volatilità realistica, i calcoli mostrano che il 90 può sicuramente essere raggiunto entro l'anno, ma che il 9 vive di più tra 25 e 45 anni in un modello neutrale, o in uno scenario di shock estremo. Hai il diritto di scommetterci, ma non è un futuro "normale", è un evento estremo, come una lunga serie di teste al casinò."
La matematica non sostituisce il nostro giudizio, ma ci impedisce di commettere errori:
Un rischio estremo con un futuro inevitabile. 🧠💪
E questo, per proteggere un portafoglio, è già enorme. 👍🚀😍🥰