Dusk Network è più di una semplice moneta per la privacy. È uno sforzo consapevole per creare una blockchain sulla quale possono avvenire transazioni finanziarie reali senza rivelare chi sta inviando cosa a chi e perché. Per raggiungere questo obiettivo, la rete si basa molto su un elenco ristretto di primitive crittografiche molto specifiche: impegni di Pedersen, Bulletproofs, EdDSA, bLSAG, firme BLS e prove a conoscenza zero in generale.
Questi non sono selezionati perché sono di moda. Sono selezionati perché ognuno di essi affronta un problema specifico che non può essere risolto da strumenti più semplici (ECDSA di base, hash di base, chiavi pubbliche di base) senza compromettere sia la privacy che le prestazioni.
Posso guidarti attraverso ogni componente e spiegarti il bisogno del mondo reale che ha guidato la sua creazione e come lavorano insieme nel design di Dusk.
1. Impegni di Pedersen – Nascondere valori pur potendo ancora dimostrare che si sommano
Supponiamo che tu voglia inviare fondi on-chain ma non vuoi che l'importo sia visibile. Tuttavia, la rete deve comunque essere in grado di verificare che il totale dell'importo di denaro in entrata sia uguale al totale dell'importo di denaro in uscita (nessuna inflazione, nessuna creazione di denaro magico).
Un semplice schema di crittografia a chiave pubblica ti permetterebbe di nascondere l'importo. Tuttavia, in tal caso non potresti mai dimostrare che i due importi nascosti si sommano a qualcosa.
Gli impegni di Pedersen risolvono esattamente questo problema.
Scegli due elementi di gruppo G e H, dove la relazione di logaritmo discreto tra H e G è sconosciuta (in pratica, H è calcolato da G tramite un hash-to-point in modo che nessuno conosca il log). Per impegnarti a un valore x, calcoli C = rG + xH.
La "magia" qui è:
Nascondere: Anche se un attaccante ha potenza di calcolo illimitata, non può risolvere x da C (poiché ciò richiederebbe di risolvere il problema del logaritmo discreto per H).
Vincolante: Non puoi aprire lo stesso C a due valori diversi (difficoltà del logaritmo discreto di nuovo).
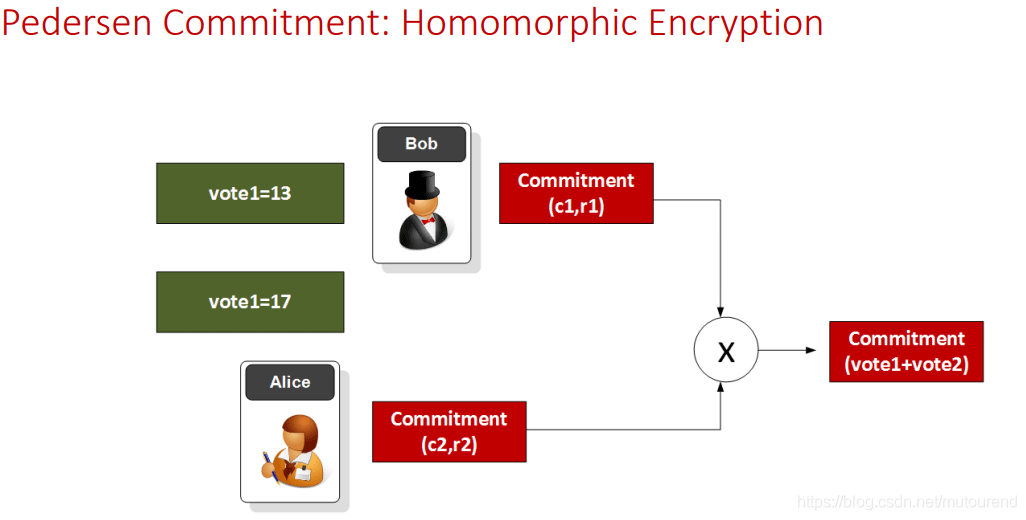
Omomorfismo additivo: C(x1, r1) + C(x2, r2) = C(x1+x2, r1+r2). Puoi aggiungere impegni senza conoscere i valori.
In Dusk, questo è utilizzato per ogni output di transazione riservata. Il mittente si impegna all'importo che sta inviando e all'importo che sta ricevendo (il resto). La rete vede solo impegni, ma può dimostrare che si sommano a zero utilizzando l'omomorfismo. Nessun importo va mai sulla catena in chiaro.
Il Pedersen vettoriale applica lo stesso concetto a più valori contemporaneamente (importo + oscuramento + campo memo + qualsiasi altra cosa tu voglia nascondere insieme). Ecco perché il documento presenta la forma vettoriale – Dusk ha spesso bisogno di impegnarsi a più scalari contemporaneamente.
2. Bulletproofs – Dimostrare "questo numero nascosto è tra 0 e 2⁶⁴" senza rivelarlo
Con numeri nascosti arriva la prossima sfida: come dimostrare che il numero è non negativo (o all'interno di un intervallo valido) senza rivelare il numero stesso?
Le prove di intervallo tradizionali (come nelle vecchie transazioni riservate in Monero prima dei Bulletproofs) erano enormi – diversi kilobyte per output.
I Bulletproofs hanno ridotto questo a ~2 KB per un intervallo di 64 bit, e, cosa importante, senza un setup fidato.
La chiave per l'efficienza dei Bulletproofs è che dimostrano affermazioni su circuiti aritmetici utilizzando prove di prodotto interno. Il provatore e il verificatore operano entrambi su vettori il cui prodotto interno rappresenta il vincolo di intervallo. La dimensione della prova è meramente logaritmica nella dimensione in bit dell'intervallo.
In Dusk, i Bulletproofs sono utilizzati per dimostrare:
Gli importi delle transazioni sono in [0, 2⁶⁴)
Calcolo corretto dell'hash di Poseidon (usato per gli impegni di nota) in un circuito
Vari altri piccoli controlli d'integrità del circuito
Poseidon è selezionato specificamente per la sua idoneità ai circuiti aritmetici (bassa profondità moltiplicativa), il che mantiene il circuito Bulletproof piccolo ed efficiente da dimostrare/verificare.
Il tempo di verifica è lineare nella dimensione del circuito, ma poiché i circuiti impiegati da Dusk sono molto piccoli (principalmente chiamate Poseidon), ciò rimane fattibile anche su hardware mobile.
3. Schemi di firma – i vari ruoli che svolgono in Dusk
EdDSA – efficiente, deterministico, autenticazione dei messaggi non malleabile
Per messaggi peer-to-peer regolari (gossip, annunci di blocco, e così via), Dusk impiega EdDSA su Curve25519.
Perché non ECDSA?
EdDSA è deterministico → nessuna cattiva casualità può rivelare la chiave privata.
La curva di Edwards distorta fornisce aritmetica più veloce e leggi di addizione complete (senza casi speciali).
La firma consiste in appena due elementi di gruppo — molto compatta ed efficiente da verificare.
È lo schema di riferimento per qualsiasi cosa che non richiede anonimato.
bLSAG (Back Linkable Spontaneous Anonymous Group signatures) – spesa anonima con protezione contro la doppia spesa
Questa è la variante della firma ad anello utilizzata per spendere biglietti.
Hai un insieme di chiavi pubbliche (l'anello). Provi di conoscere la chiave segreta per una di esse, senza rivelare quale. La dimensione della firma è costante, indipendentemente dalla dimensione dell'anello.
La linkabilità è fornita dall'immagine della chiave: un valore deterministico calcolato dalla chiave segreta, e le immagini delle chiavi sono uniche per ogni chiave. Se provi a spendere lo stesso biglietto due volte, le immagini delle chiavi corrispondono → doppia spesa rilevata.
Il componente "spontaneo" indica che non c'è un processo di setup, e chiunque può scegliere qualsiasi anello al volo. Il componente "Back" si riferisce alla soluzione di Adam Back che ha consentito la linkabilità senza compromettere l'anonimato.
Questo è ciò che consente a Dusk di avere transazioni anonime come Monero ma consente anche la rilevazione della doppia spesa on-chain.
Firme BLS – aggregazione per consenso
Le firme BLS (Boneh-Lynn-Shacham) vivono su curve amiche del pairing (BN-254 o BLS12-381). Il pairing consente l'aggregazione di molte firme in una breve firma che verifica contro la chiave pubblica aggregata.
In $DUSK , questo è applicato nel layer di consenso: centinaia di validatori possono firmare lo stesso blocco, e le loro firme vengono aggregate al volo, lasciando solo una firma on-chain. La dimensione del blocco rimane piccola anche con migliaia di firmatari.
Lo svantaggio è che le firme BLS necessitano di un setup fidato per i parametri della curva (o cerimonia MPC), ma dopo ciò, è molto potente.
4. Prove di conoscenza zero – la filosofia generale
Tutti i blocchi di costruzione sopra menzionati sono infine impiegati all'interno di prove di conoscenza zero più grandi.
Le prove di conoscenza zero di $DUSK devono soddisfare tre proprietà (che sono esplicitamente dichiarate nel documento):
Completezza – il provatore onesto convince sempre il verificatore onesto.
Solidità – il provatore disonesto non può convincere il verificatore tranne che con probabilità trascurabile.
Zero-knowledge – il verificatore non apprende nulla oltre alla verità dell'affermazione.
La spiegazione del perché queste tre proprietà siano assolutamente essenziali è semplice: in una moneta di privacy, la prova è letteralmente l'unica cosa tra la privacy finanziaria dell'utente e la completa trasparenza. Se la solidità è compromessa, allora qualcuno può stampare denaro falso. Se la conoscenza zero è compromessa, allora l'intero scopo della privacy è nullo.
Dusk impiega un mix di Bulletproofs (per prove di intervallo e circuito) e altri metodi SNARK-friendly all'interno delle sue prove di transazione. Ciò significa che l'osservatore può vedere solo la prova e gli impegni, mentre tutto il resto rimane nascosto.

Perché questo particolare insieme di strumenti?
Non è possibile fare tutto con un'unica primitiva. Pedersen ti offre anonimato + vincolo + additività. I Bulletproofs ti danno prove di intervallo e circuito efficienti su quei vincoli. bLSAG ti offre anonimato per la spesa. BLS ti offre consenso efficiente. EdDSA ti offre firme veloci per l'uso quotidiano. Si combinano tutti per creare un sistema stratificato in cui ogni strato risolve esattamente il problema che lo strato sopra non può risolvere.
Questo è il motivo per cui il design di Dusk appare "sovra-ingegnerizzato" rispetto ad altre catene più semplici – perché è un insieme di problemi più difficile da risolvere. La maggior parte delle altre catene deve rinunciare alla privacy o alla scalabilità. Dusk sta cercando di preservare entrambi, e questo richiede l'uso di questo particolare insieme di strumenti crittografici.