
« Doms? Gdzie idziemy, nie potrzebujemy domów. »
Na klasycznych rynkach mamy Depth of Market (DOM), aby zobaczyć głębokość książki zleceń: gdzie są duzi kupujący, gdzie ukrywają się sprzedawcy, jak daleko zlecenie wpłynie na cenę.
Ale na rynku Alpha… nie ma DOM. 🥶
Jak składać zlecenia w progresji geometrycznej, zarządzać ryzykiem, czuć, czy rynek jest głęboki czy płytki, kiedy nie widzimy książki? 🤔
Zrekonstruujemy głębokość implicitną na podstawie ruchu ceny między pasmami Bollingera, z małą energią dyskretną (graf / Laplacjan). 💪
1. Dlaczego DOM jest tak cenny (i co tracimy bez niego)
Na klasycznej parze Spot (BTCUSDT, ETHUSDT…), DOM daje ci:
najlepsze oferty kupna i sprzedaży,
objętości na każdym poziomie ceny,
głębokość skumulowana do ±0,1 %, ±0,5 %, ±1 %, itd.
Dla tradera, to służy do:
zidentyfikować ściany (duże bloki zleceń limit),
rozłożyć drabinę zleceń (geometria postępu wielkości/ceny),
wiedzieć, czy duże zlecenie przesunie cenę o 0,05 % czy 2 %.
Na rynku Alpha, to wszystko jest niewidoczne.😱
Widzisz tylko ślady transakcji w cenie.🤷♂️
Idea: używać tych śladów do odgadnięcia ukrytej głębokości.💪
2. Umieścić cenę w tunelu Bollingera
Zaczynamy od serii cen, w regularnych odstępach czasowych (na przykład co sekundę lub co minutę).
2.1. Średnia i ruchome odchylenie standardowe
Na oknie o długości (na przykład 20 lub 60 punktów) definiujemy:
Formuła (1) : średnia ruchoma
m_L(i) = (1 / N_L) × suma dla k od 0 do N_L − 1 z P_{i − k}
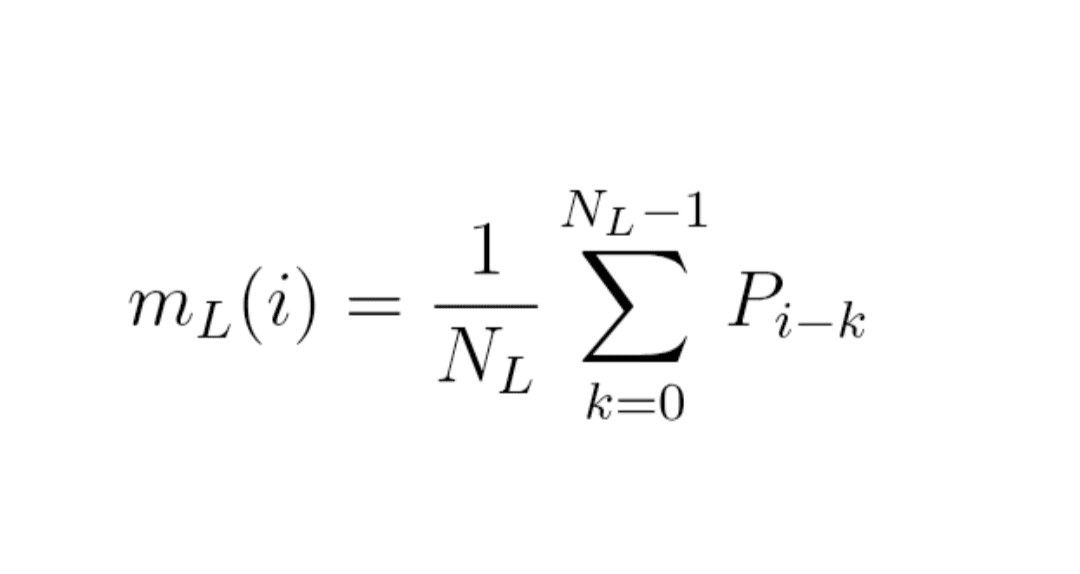
Innymi słowy,
m_L(i) = (P_i + P_{i−1} + … + P_{i−N_L+1}) / N_L.
Formuła (2) : ruchome odchylenie standardowe
σ_L(i) = pierwiastek z
[ 1 / (N_L − 1) × suma dla k od 0 do N_L − 1 z (P_{i−k} − m_L(i))² ]
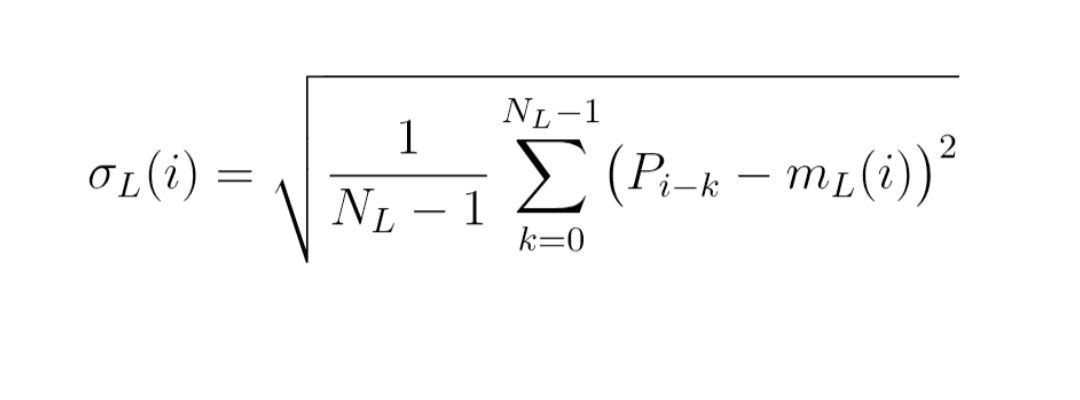
To po prostu klasyczne odchylenie standardowe, obliczone na podstawie okna przesuwnego ostatnich cen.
2.2. Bandy Bollingera
Bandy Bollingera na odchyleniach standardowych (typowo k = 2) to:
Formuła (3) : bandy
Górna banda : B_L^wysoka(i) = m_L(i) + k × σ_L(i)
Dolna banda : B_L^niska(i) = m_L(i) − k × σ_L(i)
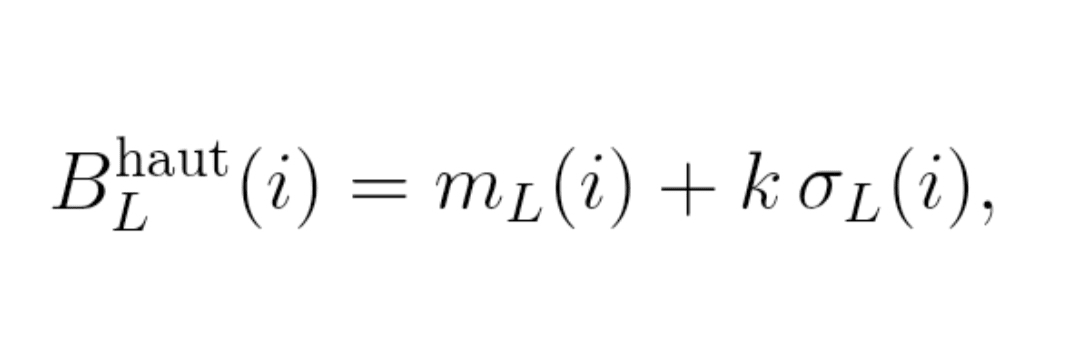
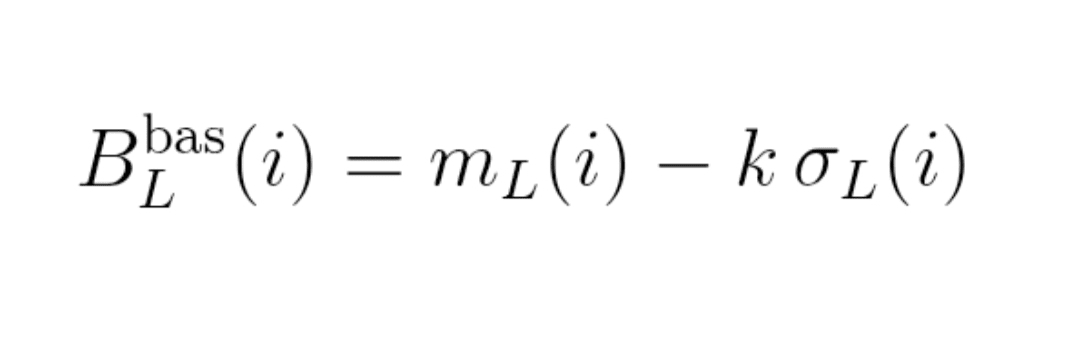
2.3. Cena znormalizowana w tunelu
Patrzymy następnie, gdzie znajduje się cena w liczbie sigma:
Formuła (4) : cena znormalizowana
z_L(i) = (P_i − m_L(i)) / σ_L(i)
z_L(i) ≈ 0 : cena w centrum tunelu,
|z_L(i)| ≈ 1, 2, 3 : cena zbliża się do lub dotyka band.
Wszystko, co następuje, dzieje się w tym znormalizowanym układzie z_L.
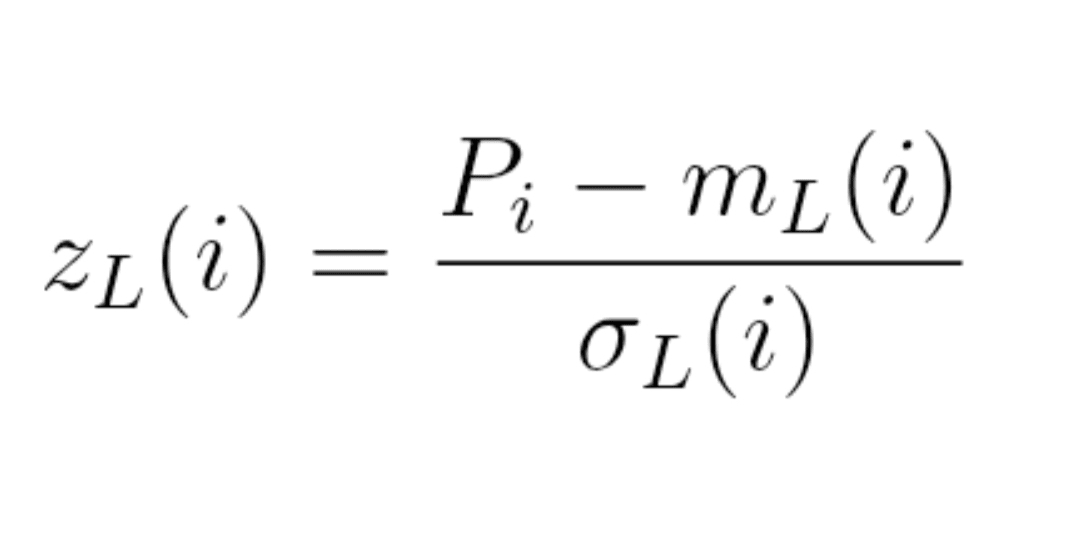
3. Mierzyć „chropowatość” ceny między bandami
Intuicja:
Głęboki rynek → cena płynnie przesuwa się w swoim tunelu.
Rynek płytki → cena jest nerwowa, poszarpana, skacze bardzo szybko z jednego boku do drugiego tunelu.
Mierzymy tę chropowatość za pomocą dyskretnej energii Dirichleta.
Umieszczamy się na oknie wskaźników od i_0 do i_1.
Formuła (5) : energia E_L
E_L(i_0, i_1)
= 1/2 × suma dla i od i_0 do i_1 − 1 z [ z_L(i+1) − z_L(i) ]²
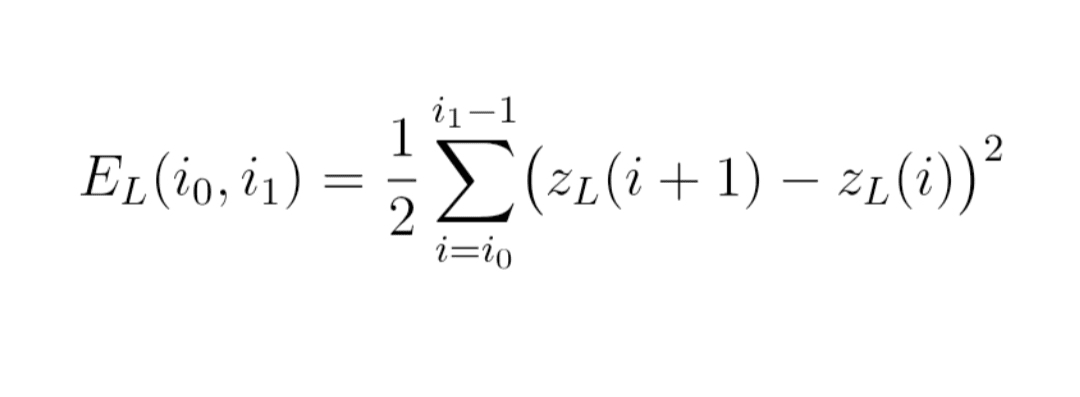
Następnie normalizujemy przez długość okna, aby uzyskać gęstość:
Formuła (6) : gęstość energii ε_L
ε_L(i_0, i_1) = E_L(i_0, i_1) / (i_1 − i_0)
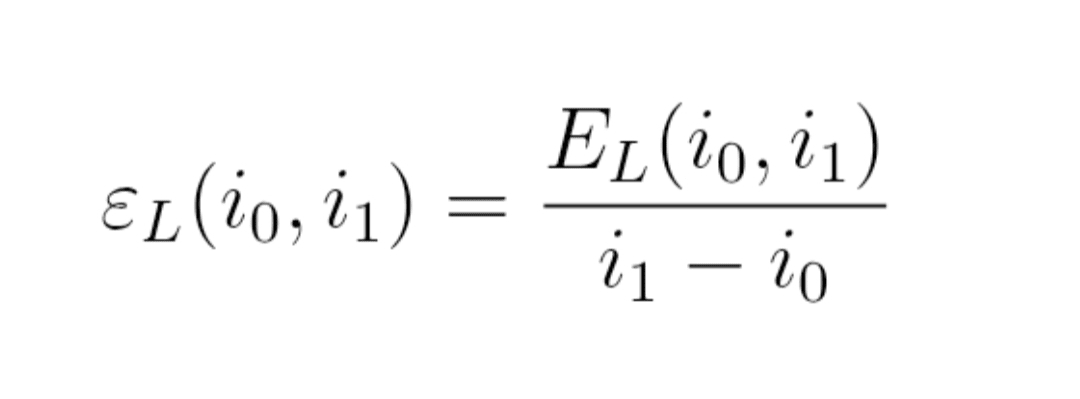
Odczyt:
ε_L małe → trajektoria z_L dość gładka,
ε_L duże → trajektoria z_L bardzo poszarpana.
Ogólnie, ε_L mierzy, jak bardzo cena „skacze” wewnątrz swojego tunelu Bollingera, niezależnie od skali cenowej (dzięki normalizacji przez σ_L).
4. Głębokość implikowana: prosty wynik Λ_L
Teraz chcemy połączyć tę chropowatość z głębokością rynku.
4.1. Mały model stylizowany
Zauważamy:
Formuła (7) : podstawowa stopa zwrotu
r_i = log(P_{i+1}) − log(P_i)
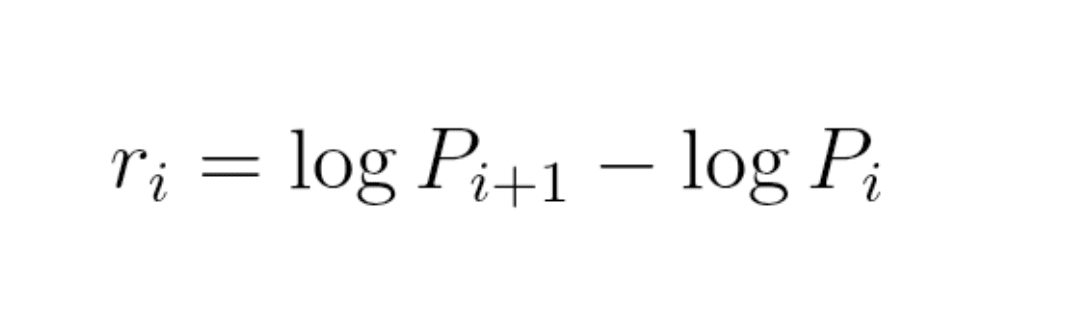
Zakładamy bardzo prosty model:
Formuła (8) : model mikrostrukturalny
r_i = (1 / Λ_i) × q_i + η_i
gdzie:
q_i = nierównowaga zleceń (zakupy rynkowe − sprzedaże rynkowe) na przedziale,
Λ_i = lokalna głębokość rynku,
η_i = „szum” (wiadomości, przepływy fundamentalne…).
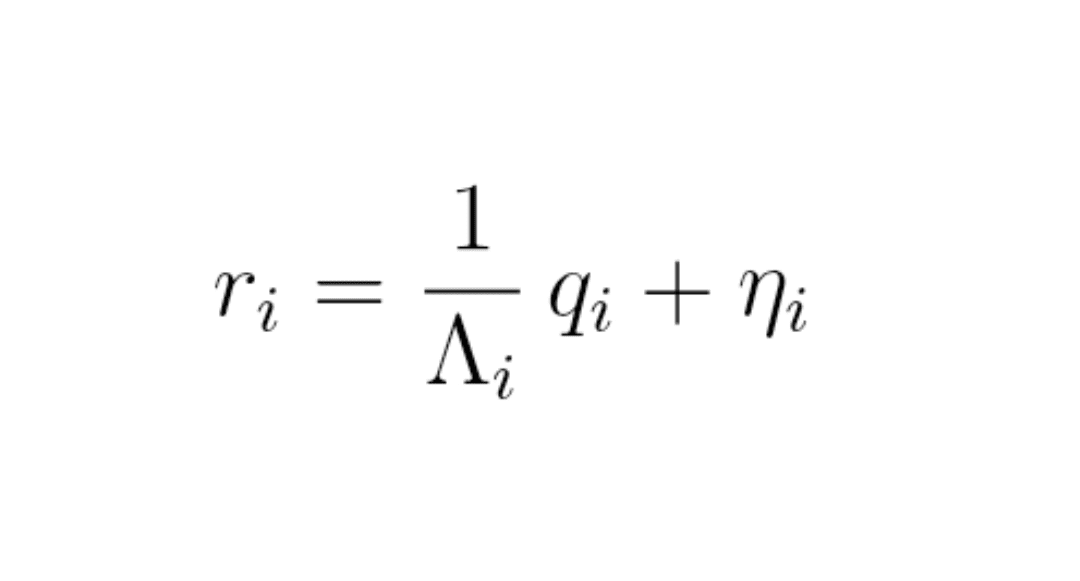
Bez DOM nie widzimy ani q_i ani Λ_i.
Ale widzimy r_i, więc z_L, więc ε_L.
Rozważając wariancje i grupując stałe, dochodzimy do relacji tego typu:
Formuła (9) : wariancja stóp zwrotu (schemat)
E[r_i²] ≈ σ_q² / Λ² + σ_η²
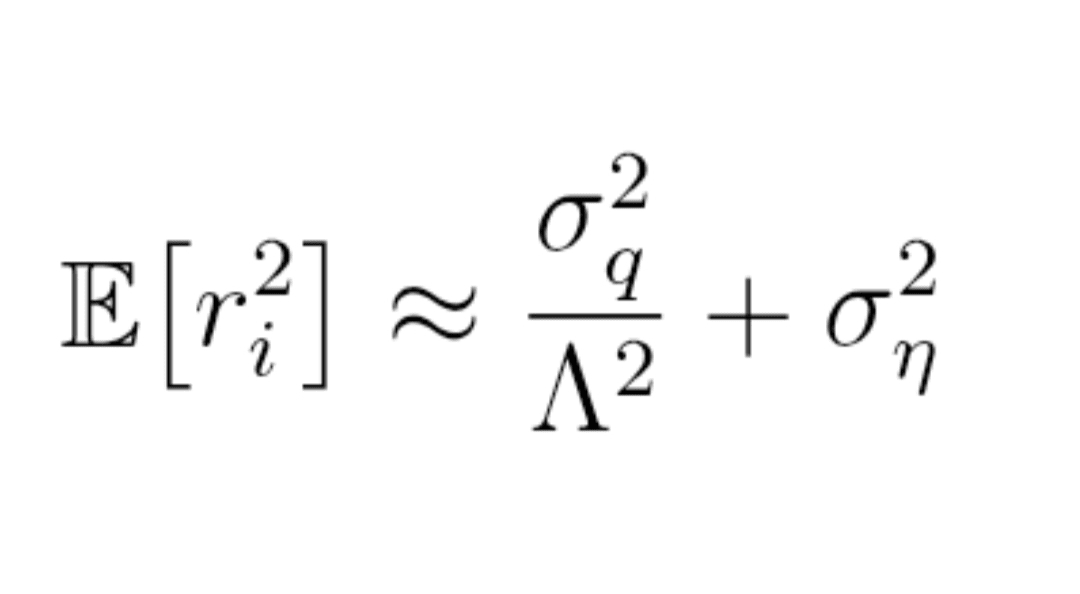
(średnio na oknie, σ_q i σ_η są stałymi, Λ to typowa głębokość).
Kluczowa idea: im mniejsze Λ, tym większy człon σ_q² / Λ², więc większe r_i² → cena jest bardziej wzburzona przy tym samym przepływie zleceń.
Łącząc z_L i r_i (z_L to mniej więcej stopa zwrotu podzielona przez σ_L), uzyskujemy, że ε_L rośnie, gdy Λ maleje.
Stąd bardzo prosty wynik głębokości implikowanej 👇
4.2. Praktyczna definicja wyniku Λ_L
Formuła (10) : wynik głębokości implikowanej
Λ_L ≈ C_L × σ_L / pierwiastek z ε_L
gdzie:
σ_L = lokalna zmienność,
ε_L = gęstość energii,
C_L = stała do kalibracji na parze, gdzie DOM jest widoczny.
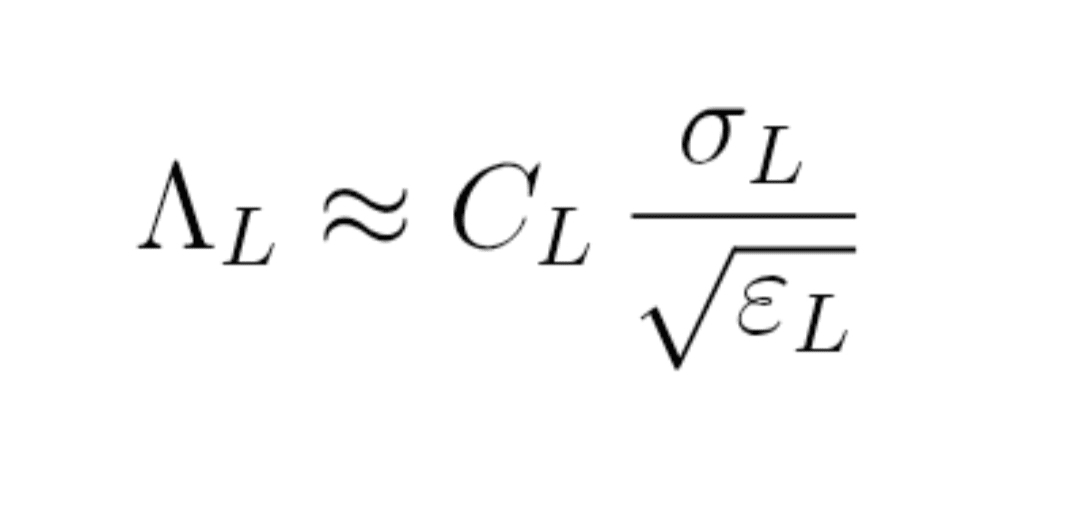
Odczyt:
Λ_L duże → rynek dobrze absorbuje przepływy zleceń → duża głębokość.
Λ_L małe → cena „trzęsie się” dużo dla tego samego σ_L → rynek płytki.
Masz teraz wskaźnik głębokości implikowanej bez widzenia książki zleceń. 🤩
5. Objętość implikowana do band
W wielu modelach mikrostrukturalnych, objętość potrzebna do przesunięcia ceny o pewne Δp jest proporcjonalna do Λ_L × |Δp|.
Jeśli patrzymy na to, co się dzieje aż do band na k odchyleniach standardowych:
Δp = k × σ_L.
Możemy wtedy zdefiniować objętość implikowaną do band:
Formuła (11) : objętość implikowana V_L^imp
V_L^imp (Δp = k σ_L)
≈ k × C_L × σ_L² / pierwiastek z ε_L
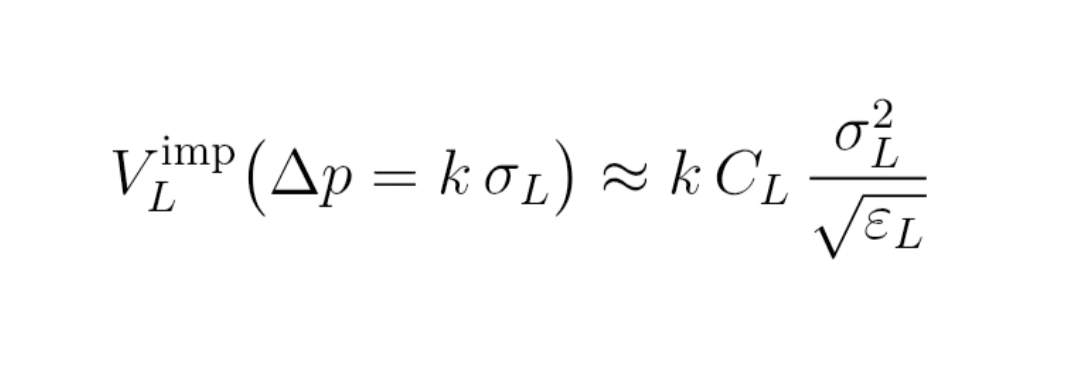
Ta V_L^imp jest rzędem wielkości objętości, którą należałoby (średnio) do przeszukiwania ukrytej książki zleceń aż do band Bollingera.
Na parze z DOM możesz porównać:
V_L^imp ↔ rzeczywista skumulowana objętość w książce zleceń.
Na rynku Alpha masz tylko V_L^imp… ale to już kompas. 🧭
6. Jak to wdrożyć na Binance
6.1. Faza 1 : kalibracja na parze z widocznym DOM
1. Wybierz bardzo płynną parę (BTCUSDT, ETHUSDT Spot).
2. Na żywo:
zbiera ceny (transakcje lub świeczki 1s),
zbiera zrzuty DOM (głębokość skumulowana do ±0,1 %, ±0,5 %, ±1 %, itd.).
3. Dla każdego okna:
oblicz m_L, σ_L, ε_L,
oblicz surowy wskaźnik S_L = σ_L² / pierwiastek z ε_L,
mierzy rzeczywistą objętość V_obs skumulowaną w DOM do Δp = k σ_L.
4. Wykonaj prostą regresję:
Formuła (12) : relacja empiryczna
V_obs ≈ C_L × S_L
(z S_L = σ_L² / √ε_L)
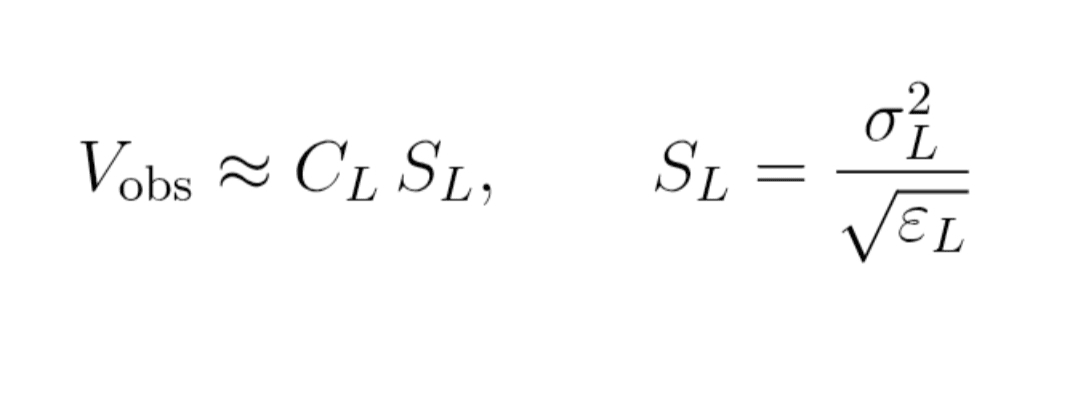
Możesz wywnioskować stałą C_L dla tej skali L.
6.2. Faza 2 : zastosowanie na rynku Alpha (bez DOM)
1. Na twojej parze Alpha:
zbiera ceny na żywo,
oblicz m_L, σ_L, ε_L.
2. Zastosuj formułę:
Formuła (13) : ostateczna objętość implikowana
V_L^imp (Δp = k σ_L) ≈ k × C_L × σ_L² / √ε_L
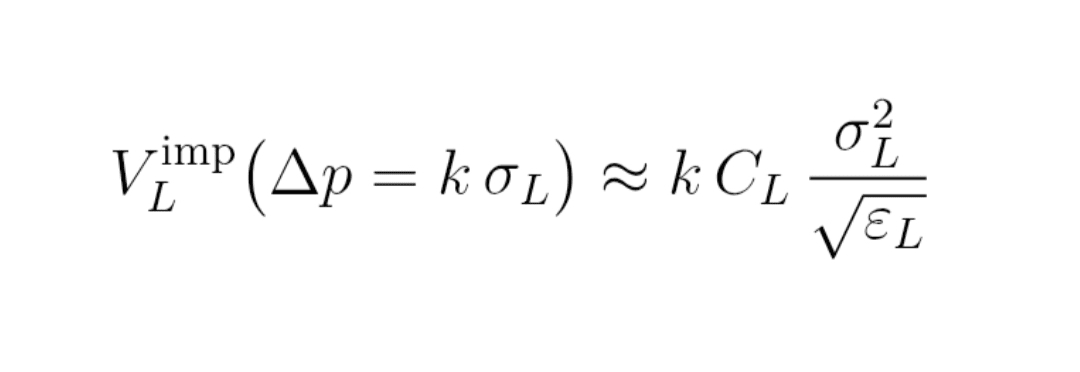
3. Wyświetlaj w czasie rzeczywistym:
wynik Λ_L,
krzywa Δp ↦ V_L^imp (twój fantomowy DOM).
7. Konkretny przykład zastosowania dla twoich zleceń
7.1. Zbudować drabinę zależną od Λ_L
Jeśli Λ_L jest wysokie: rynek głęboki,
możesz:
zbliżyć poziomy twojego postępu geometrycznego,
utrzymywać rozmiary zleceń dość regularnych.
Jeśli Λ_L jest niskie: rynek płytki,
możesz:
jeszcze bardziej oddalić poziomy,
zmniejszyć rozmiar zleceń blisko ceny,
utrzymaj objętość dla bardziej odległych poziomów.
7.2. Czytanie „dziur w płynności” implikowanych
Patrząc na Λ_L w czasie rzeczywistym:
Λ_L gwałtownie spada, podczas gdy σ_L nie zmienia się zbytnio:
ostrzeżenie: rynek staje się kruchy,
możesz zmniejszyć dźwignię, poszerzyć stop lossy, unikać zbyt agresywnego „rynku”.
Λ_L rośnie po wstrząsie:
znak odporności: głębokość wraca, rynek zyskuje.
8. Limity i zdrowy rozsądek
To nie jest wyrocznia:
nie widzi spoofersów,
nie uwzględnia wiadomości makroekonomicznych,
nie zastępuje twojego zarządzania kapitałem.
Wskaźnik zależy:
wyboru okna N_L,
jakości kalibracji C_L,
granularności danych.
Do użycia jako:
radar głębokości implikowanej, w uzupełnieniu do twojej analizy technicznej,
nie jako magiczny przycisk „kup/sprzedaj”.
9. Aby pójść dalej
Ten artykuł daje wersję „tradera”.
Za tym kryje się mała teoria:
funkcja z_L widziana jako funkcja na łańcuchu (grafie),
energia Dirichleta,
połączenie z równaniem ciepła i stopniowym wygładzaniem.
W oddzielnym artykule matematycznym można szczegółowo omówić to wszystko w odpowiedni sposób, z dowodami na koncie TikTok @Maths4Traders 💪🤩

