#RumorsVSTruth
#ProbabilityCalculations
#IntroductionToResilientMathematics
Es gibt immer diesen Moment, mitten im Krypto-Markt, wo jemand sehr selbstsicher sagt:
„Du wirst sehen, SOL geht auf 9, das steht geschrieben.“
Und manchmal kommt auch die „sanfte“ Version dazu:
„Und 90 auch, das ist im Visier.“
Zum Zeitpunkt (des Anfangs 😅) des Schreibens dieses Artikels war SOL bei etwa 135 USDC.
Unser Gehirn sieht also drei Zahlen: 135, 90, 9… und stellt sich eine Treppe vor: 135 → 120 → 100 → 90 → 60 → 30 → 9.
Das Problem ist, dass die Märkte nicht im „arithmetischen Treppenmuster“ funktionieren (man zieht X Dollar ab), sondern multiplikativ (man multipliziert mit 0,7, 0,5, 0,1…).
Die Mathematik arbeitet mit Logarithmen und Wahrscheinlichkeiten.
Ziel dieses Artikels:
1. Zeige, warum 90 und 9 in Bezug auf die Wahrscheinlichkeit nichts gemeinsam haben.
2. Schätzen, in wie viel Zeit jeder dieser Niveaus mehr als 50 % Wahrscheinlichkeit hat, erreicht zu werden, in einem vernünftigen Modell.
3. Vergleiche das mit einem Kopf oder Zahl, um die Intuition neu zu kalibrieren.
4. Integrieren:
der Angst- und Gierindex,
die multiwährungs DoM (USDC, EUR usw.).
5. Beenden mit einer resilienten Lesart von SOL über verschiedene Zeitrahmen.
1. Erste Falle: Unser Gehirn ist linear, der Markt ist es nicht
Wir starten von einem Referenzpreis:
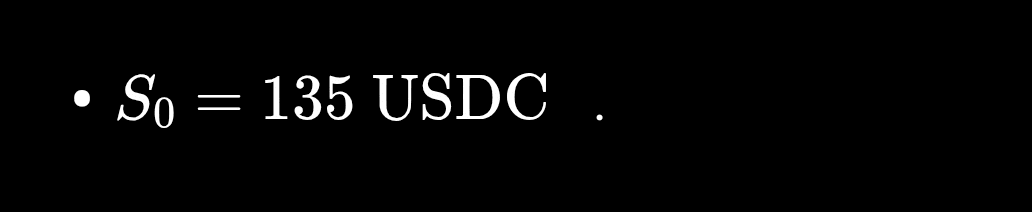
Zwei Ziele stehen zur Diskussion:

In Prozent:
135 → 90 : Rückgang von etwa 33 %.
135 → 9 : Rückgang von etwa 93 %.
Unsere Intuition erzählt etwas wie:
„90 ist die strenge Version, 9 ist die extreme Version derselben Geschichte.“
Es sei denn, in der Finanzwelt denkt man nicht in „+ oder − X Dollar“, sondern in Verhältnissen.
Wir betrachten den Logarithmus des Preises, da die prozentualen Änderungen sich im Log addieren.

Sofortiges Fazit:
Im „log Raum“ ist 9 etwa 2,708 / 0,405 ≈ 6,7 Mal weiter weg als 90.
9 ist nicht "ein Stück unter 90", es ist ein anderer Kontinent.
Und wie wir sehen werden, ist die typische Zeit, um eine Distanz in einer Zufallsbewegung zu erreichen, proportional zu d².
Also, bei gegebener Volatilität ist der Horizont, um 9 zu erreichen, ungefähr:
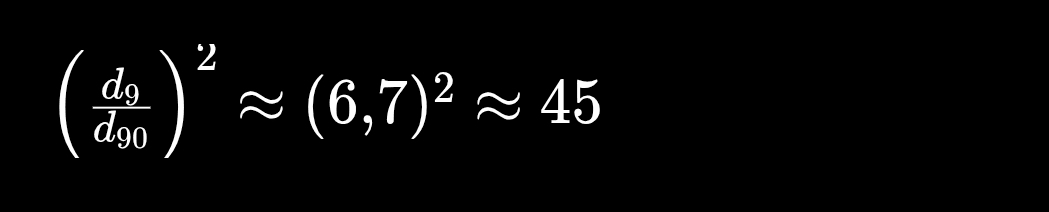
→ etwa 45 Mal länger als um 90 zu erreichen.
2. Der Rahmen: realistische Volatilität und Zufallsbewegung
Wir geben uns ein einfaches, aber standardmäßiges Modell in der Finanzwelt.


(also 60–80 % annualisierte Volatilität), was für ein nervöses L1 in der Krypto realistisch ist.
3. Grundformel: Wahrscheinlichkeit, ein Niveau vor T zu erreichen

wo Φ die Verteilungsfunktion der Standardnormalverteilung ist.
In Worten:

Wir wissen, dass:

Das ist die Schlüssel-Formel, die wir verwenden werden, um 90 und 9 zu vergleichen.
4. 90 gegen 9: typische Zeitrahmen
Erinnerung:

4.1. Typische Zeit, um 90 zu erreichen:
Wir verwenden die folgende allgemeine Formel für die Zeit T50(L), das heißt, den Horizont, für den die Wahrscheinlichkeit, das Niveau L zu erreichen, 50 % beträgt:
T50(L) ≈ [ d(L) / (0,674 × σ) ]²
wo:
d(L) = ln(S0 / L) ist die Distanz im Log-Preis,
σ ist die annualisierte Volatilität (hier zwischen 0,6 und 0,8),
0,674 ist eine Konstante, die aus dem Normalgesetz stammt (Quantil bei 75 %).
Für das Niveau L = 90, mit S0 = 135:
d(90) = ln(135 / 90) ≈ ln(1,5) ≈ 0,405.
Wir berechnen T50(90) für zwei Werte von σ.
1. Wenn σ = 0,6:
0,674 × 0,6 ≈ 0,404
d(90) / (0,674 × σ) ≈ 0,405 / 0,404 ≈ 1,002
T50(90) ≈ (1,002)² ≈ 1,0 Jahr
2. Wenn σ = 0,8:
0,674 × 0,8 ≈ 0,539
d(90) / (0,674 × σ) ≈ 0,405 / 0,539 ≈ 0,75
T50(90) ≈ (0,75)² ≈ 0,56 Jahre
Praktisches Fazit:
T50(90) liegt grob zwischen 0,6 und 1,0 Jahren.
Anders gesagt, in einem neutralen, aber volatilen Markt ist es statistisch ziemlich plausibel, dass SOL mindestens einmal im Jahr 90 erreicht (Wahrscheinlichkeit über 50 %).
4.2. Typische Zeit, um 9 zu erreichen: T50(9)
Wir wenden genau dieselbe Formel auf L = 9 an.
Immer mit S_0 = 135, haben wir:
d(9) = ln(135 / 9) = ln(15) ≈ 2,708.
Wir berechnen T50(9) für dieselben Werte von σ.
1. Wenn σ = 0,6:
0,674 × 0,6 ≈ 0,404
d(9) / (0,674 × σ) ≈ 2,708 / 0,404 ≈ 6,71
T50(9) ≈ (6,71)² ≈ 44,8 Jahre
2. Wenn σ = 0,8:
0,674 × 0,8 ≈ 0,539
d(9) / (0,674 × σ) ≈ 2,708 / 0,539 ≈ 5,02
T50(9) ≈ (5,02)² ≈ 25,2 Jahre
Praktisches Fazit:
T50(9) liegt zwischen etwa 25 und 45 Jahren.
Anders gesagt, im selben neutralen Modell mit realistischer Volatilität würde es mehrere Jahrzehnte dauern, damit „SOL ≤ 9 mindestens einmal“ eine Wahrscheinlichkeit von 50 % hat. Es ist ein extremes Szenario, sehr weit entfernt von einem „natürlichen Ziel“ auf kurze oder mittlere Sicht.
Und außerdem haben wir einen möglichen langfristigen Aufwärtsdrift (Adoption, Netzwerkgewinne…) nicht berücksichtigt, der 9 noch weniger wahrscheinlich machen würde.
5. Wahrscheinlichkeiten über feste Horizonte (1 Jahr, 5 Jahre)
Mit der Formel:
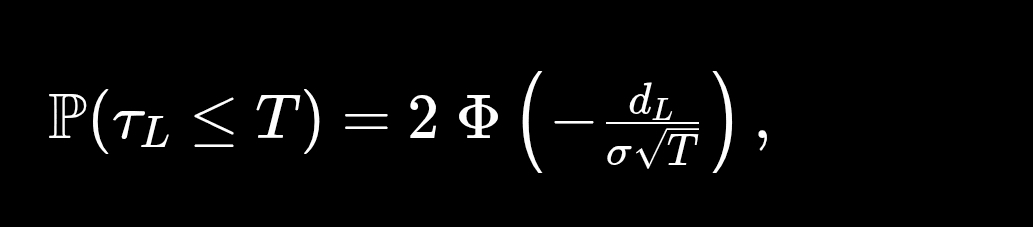
man kann auch Größenordnungen für einen festgelegten Horizont geben (zum Beispiel 1 Jahr, 5 Jahre).
Nehmen wir zum Beispiel eine mittlere Volatilität:

Also:
Über 1 Jahr ist 90 ein nahezu „Kopf oder Zahl“-Szenario (etwas über 50 %),
während 9 auf etwa 0,01 % steht, das heißt, ein echtes Ereignis in der Verteilungsschwänze.
Über 5 Jahre wird 90 sehr wahrscheinlich (etwa 80 %),
9 bleibt überwiegend minoritär (~8 %).
6. Vergleich von Kopf oder Zahl
Um unsere Intuition zu kalibrieren, vergleichen wir mit einer einfachen Erfahrung: einer ausgewogenen Münze.
Wahrscheinlichkeit, mindestens einen Kopf in n Würfen zu haben:

Die Analogie:
„SOL innerhalb eines Jahres zu sehen, ist in einem volatilen Markt“
→ das ist die Art eines alltäglichen Ereignisses, wie mindestens „eine Kopf“ in ein paar Würfen zu haben.
„SOL innerhalb eines Jahres zu sehen, im selben Modell“
→ das ist auf dem Niveau einer sehr unwahrscheinlichen Serie von aufeinanderfolgenden Köpfen (wie 12–13 hintereinander).
Also:
Zu sagen „SOL geht auf 9“, weil wir gerade einen großen Rückgang erlebt haben, ist ein bisschen wie zu sagen „Ich werde sicher 13 Köpfe hintereinander haben“, weil du gerade drei Würfe verloren hast.
Menschlich… aber sehr weit entfernt von dem, was die Wahrscheinlichkeiten sagen.
7. Wo platzieren wir den Angst- und Gierindex?
Der Angst- und Gierindex (Fear & Greed Index) misst die Marktstimmung auf 0–100:
0–25: extreme Angst,
25–50: Angst,
50–75: Neutralität / moderate Optimismus,
75–100: extreme Gier.
Er wird berechnet aus:
die jüngste Volatilität,
die Volumina und Auftragsflüsse,
die Dominanz von BTC,
die Google-Recherchen,
die Aktivität in sozialen Medien usw.
Es ist also konzeptionell sehr mit unserem σ verbunden: je stärker die Angst, desto höher ist die beobachtete Volatilität.
Man kann nach Regimen denken:
1. „Normales“ Regime (Index zwischen 30 und 70)
→ Volatilität in einem Bereich von 60–80 % für SOL.
→ das ist das Regime unserer Hauptberechnungen:
90 plausibel innerhalb des Jahres,
9 ultra selten.
2. Regime extremer, verlängerter Angst (nachhaltiger Index < 25)
→ effektive Volatilität, die bis zu 100–150 % steigen kann.
→ die Schwänze der Verteilung (extreme Bewegungen) sind dicker.
Wenn man zum Beispiel nimmt:

Die Wahrscheinlichkeit, 9 in 1 Jahr zu erreichen, würde steigen (wir würden aus 0,01 % herauskommen), bliebe aber sehr weit von einem zentralen Szenario entfernt.
Zusammenfassend:
Ja, lange Perioden der Angst komprimieren die Zeit, die notwendig ist, um niedrige Niveaus zu erreichen.
Nein, sie reichen nicht aus, um 9 in ein „natürliches Ziel“ auf kurze Sicht zu verwandeln.
Das Gehirn nimmt den Angstindex und projiziert sich in den Katastrophenmodus (selbst mein Gehirn wird oft hereingelegt 🧠😅).
Die Mathematik betrachtet die gesamte Verteilung und den Horizont.
8. DoM in USDC, DoM in EUR: Aufholjagd des Verhaltens
Der Vergleich der DoM in Euro und in USDC (ich habe eine Bestellung zu 100 € platziert 😉) liefert uns eine relevante Information (ich bin mir sicher, dass Ihr Unterbewusstsein das bereits gespürt hat, nicht wahr? 🤩
Jedes Paar hat sein eigenes „psychologisches Universum“:
SOL/USDC → Referenzen in Dollar (100, 90, 80…).
SOL/EUR → Referenzen in Euro (100 €, 80 €…).
SOL/BTC → Referenzen in Bruchstücken von BTC usw.
Auf jedem Orderbuch bauen Händler Auftragsmauern (Bid/Ask) um diese Referenzpunkte.
Aber all diese Märkte sind durch Arbitrage verbunden:
wenn SOL/EUR „zu niedrig“ im Vergleich zu SOL/USDC ist (einmal den EUR/USD-Kurs berücksichtigt),
Bots werden in EUR kaufen und in USDC verkaufen, und umgekehrt.
Das schafft eine dauerhafte Anpassung, bei der Fehler und lokale Verschiebungen korrigiert werden und somit die großen Liquiditätszonen (100 €, 90–95 $, 0,00X BTC…) schließlich ausgerichtet werden.
Das Kreuzen der DoM in mehreren Währungen ermöglicht es also: die globalen Treppenstufen des Marktes zu erkennen, zu sehen, wo die Aufträge wirklich weltweit konzentriert sind, zu vermeiden, von einer einzigen Zahl (zum Beispiel nur "9") hypnotisiert zu werden.
In einem resilienten Ansatz lieben wir das: wir suchen nach Strukturen, die sichtbar bleiben, selbst wenn wir die Währung, den Maßstab oder den Standpunkt ändern.
9. Resiliente Lesart von SOL: kurz-, mittel-, langfristig
Um abzuschließen, wenden wir unsere Intuition resilienter Mathematik an.
Vereinfachte Idee einer „resilienten Ableitung“ auf einer Zeitskala:

→ Das ergibt eine Art robustes Wachstum in diesem Maßstab.
Ohne in eine komplexere Formel einzutauchen, verwenden wir sie als qualitative Lesart.
9.1. Kurzfristig (einige Tage bis einige Wochen)
In diesem Maßstab:
die resiliente Ableitung ist sehr volatil,
ein großer Rückgang macht sie brutal negativ,
ein technischer Rückschlag kann sie schnell wieder nach oben bringen.
Die relevanten Szenarien sind:
Bereiche, die mit der Liquiditätsstruktur verbunden sind (z.B. 135–145),
von Mikro-Trends, die durch die Mauern des Orderbuchs gesteuert werden.
Auf diesem Zoom-Level macht die Frage „9 oder 90?“ einfach keinen Sinn.
Wir sind im Geräuschmanagement, Unterstützung/Widerstand, Liquidationen.
9.2. Mittelfristig (6 bis 18 Monate)
Hier ist die resiliente Ableitung:
glättet einen Teil des Rauschens,
integriert die Zyklen von Angst/Gier,
beginnt, die tatsächliche Annahme des Ökosystems widerzuspiegeln.
In diesem Rahmen, für Solana:
90 in einem Volatilitätszyklus zu besuchen, ist statistisch normal (wir haben gerade gesehen, dass es 50–60 % in 1 Jahr in einem neutralen Modell ist).
9 zu besuchen bleibt ein Szenario in der Verteilungsschwänze, verbunden mit:
ein Zusammenbruch des Vertrauens,
eine Regulierung oder ein großes Skandal,
ein strukturelles Problem.
Ohne größere Schocks sagen uns die Mathematik, dass über 6–18 Monate:
90 gehört zum „lebendigen“ Teil der Verteilung,
9 bleibt in der extremen Schwänze gefangen.
9.3. Langfristig (mehrere Jahre)
Langfristig betrachtet, schaut die resiliente Ableitung:
der Platz von Solana im Ökosystem (DeFi, NFT, Spiele, RWA…),
die technische Stabilität,
der Wettbewerb der anderen L1/L2,
die Netzwerkgewinne usw.
Zwei große Szenarien:
1. Resilientes bullisches Szenario
Solana behält eine wichtige Rolle,
→ resiliente positive Steigung bei 3–5 Jahren,
→ 9 wird zu einem „historischen“ Niveau statt einem Ziel,
→ Rückgänge bleiben möglich, aber eine dauerhafte Rückkehr zu 9 wäre mit einem außergewöhnlichen Ereignis verbunden.
2. Strukturell bärisches Szenario
Solana fällt ab,
→ resiliente negative Steigung auf lange Sicht,
→ sehr niedrige Niveaus (einschließlich 9) werden auf sehr lange Sicht wieder zugänglich,
→ aber in einer "anderen Geschichte" von Solana als der, die wir heute kennen.
Die Mathematik sagt nicht, welches Szenario eintreten wird. 😭
Sie sagen: „Hier ist der Platz jedes Szenarios in der Verteilung der Möglichkeiten.“
10. Fazit: Was die Mathematik in unser Intuition korrigiert
Indem wir zusammenfassen:
das Modell der Volatilität,
der Vergleich der log-Distanzen (90 gegen 9),
die Horizonte,
der Effekt des Angst-/Gier-Index,
die multiwährungs DoM,
und eine resiliente Mehrschichtenlesung,
wir erhalten ein klares Fazit:
1. 90 und 9 sind keine zwei "Stufen" auf derselben Skala.
Im Log-Preis ist 9 6,7 Mal weiter entfernt als 90, und etwa 45 Mal „weiter“ in typischer Zeit.
2. Über 6–12 Monate,
90 ist plausibel,
9 ist nahezu unmöglich in einem Modell realistischer Volatilität ohne größeren Schock.
3. Über 5 Jahre,
90 wird fast sicher (80 % in unserem Beispiel),
9 bleibt ein Minderheitsevent (~8 %).
4. Der Angst-/Gier-Index erklärt, warum die Gemüter nach unten ausbrechen, invalidiert jedoch nicht die Statistik.
Angst ist ein Regime, keine Prophezeiung.
5. Das Kreuzen der DoM in mehreren Währungen offenbart die wahren globalen Konsenszonen, anstatt sich an einer isolierten Zahl festzuhalten.
6. Der resiliente Ansatz platziert jedes Szenario entsprechend dem Horizont (kurz, mittel, langfristig).
Angesichts des „kleinen Schlauberger“, der behauptet:
„SOL strebt 9 zu.“
man kann ruhig antworten:
„Mit realistischer Volatilität zeigen die Mathematiken, dass 90 durchaus im Laufe des Jahres besucht werden kann, aber dass 9 eher bei 25–45 Jahren in einem neutralen Modell oder in einem extremen Schockszenario lebt. Du hast das Recht, darauf zu wetten, aber das ist keine 'normale' Zukunft, es ist ein Schwankungsereignis, wie eine lange Serie von Köpfen im Casino.“
Die Mathematik ersetzt nicht unser Urteil, aber sie hilft uns, nicht zu verwechseln:
ein extremes Risiko mit einer unvermeidlichen Zukunft. 🧠💪
Und das, um ein Portfolio zu schützen, ist schon enorm.👍🚀😍🥰

