
« Doms? Wohin wir gehen, brauchen wir keine Doms. »
Auf den klassischen Märkten haben wir ein Depth of Market (DOM), um die Tiefe des Orderbuchs zu sehen: wo die großen Käufer sind, wo die Verkäufer sich verstecken, bis wohin ein Auftrag den Preis treiben wird.
Aber auf dem Alpha-Markt… gibt es kein DOM. 🥶
Wie man seine Aufträge in geometrischer Progression platziert, sein Risiko verwaltet, spürt, ob der Markt tief oder flach ist, wenn man das Orderbuch nicht sieht? 🤔
Wir werden eine implizite Tiefe basierend auf der Preisbewegung zwischen den Bollinger-Bändern rekonstruieren, mit einer kleinen diskreten Energie (Graph / Laplacian). 💪
1. Warum das DOM so wertvoll ist (und was wir ohne es verlieren)
Auf einem klassischen Spot-Paar (BTCUSDT, ETHUSDT…) gibt dir das DOM:
die besten Gebote und Angebote,
die Volumina auf jeder Preisstufe,
die kumulierte Tiefe bis ±0,1 %, ±0,5 %, ±1 %, usw.
Für einen Trader dient es dazu:
erkenne die Walls (große Blöcke von Limit-Orders),
eine Treppe von Orders (geometrische Fortschrittsfolge von Größen/Preisen) verteilen,
wissen, ob eine große Order den Preis um 0,05 % oder 2 % bewegen wird.
Auf dem Alpha-Markt ist all dies unsichtbar.😱
Du siehst nur die Spuren der Transaktionen im Preis.🤷♂️
Die Idee: Diese Spuren zu nutzen, um die verborgene Tiefe zu erraten.💪
2. Setze den Preis in einen Bollinger-Tunnel
Wir beginnen mit einer Preisserie, mit regelmäßigen Zeitabständen (zum Beispiel jede Sekunde oder jede Minute).
2.1. Gleitende Mittelwerte und Standardabweichungen
Über ein Fenster von Länge (zum Beispiel 20 oder 60 Punkten) definiert man:
Formel (1) : gleitender Durchschnitt
m_L(i) = (1 / N_L) × Summe für k von 0 bis N_L − 1 von P_{i − k}
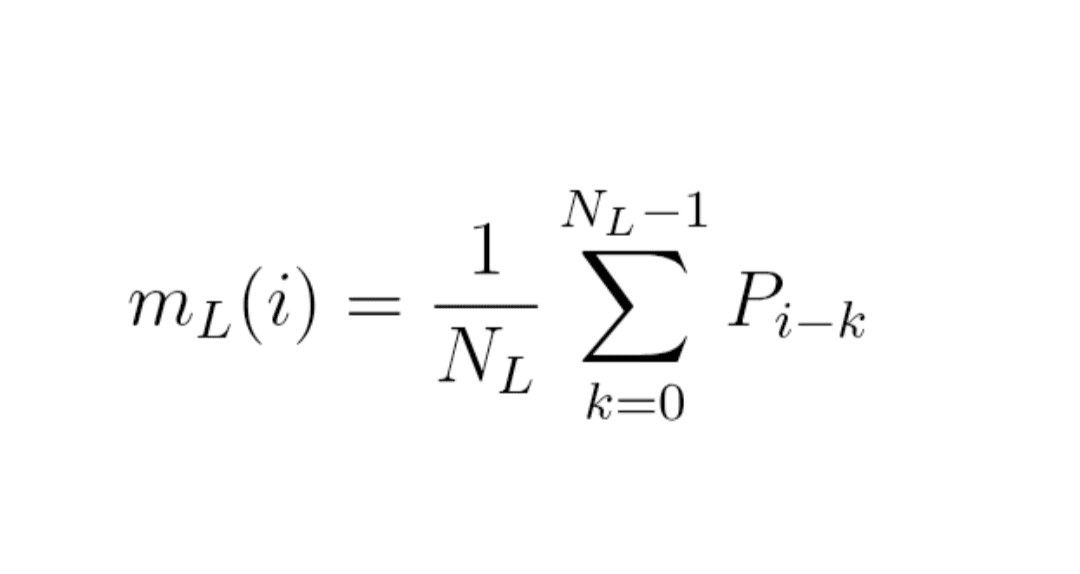
Anders ausgedrückt,
m_L(i) = (P_i + P_{i−1} + … + P_{i−N_L+1}) / N_L.
Formel (2) : gleitende Standardabweichung
σ_L(i) = Quadratwurzel von
[ 1 / (N_L − 1) × Summe für k von 0 bis N_L − 1 von (P_{i−k} − m_L(i))² ]
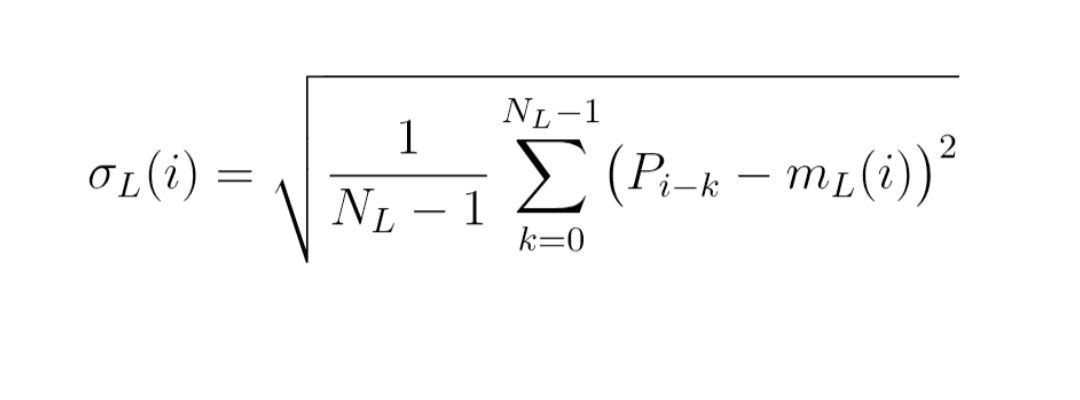
Das ist einfach die klassische Standardabweichung, berechnet über das gleitende Fenster der letzten Preise.
2.2. Bollinger-Bänder
Die Bollinger-Bänder bei Standardabweichungen (typischerweise k = 2) sind:
Formel (3) : Bänder
Obere Band: B_L^hoch(i) = m_L(i) + k × σ_L(i)
Untere Band: B_L^niedrig(i) = m_L(i) − k × σ_L(i)
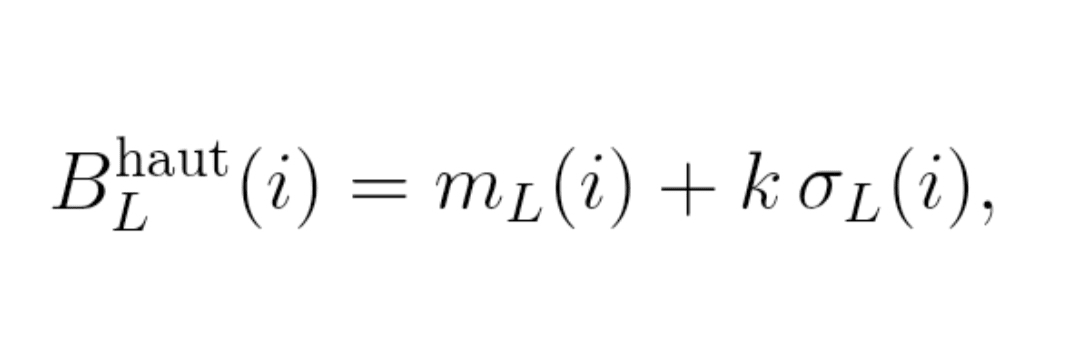
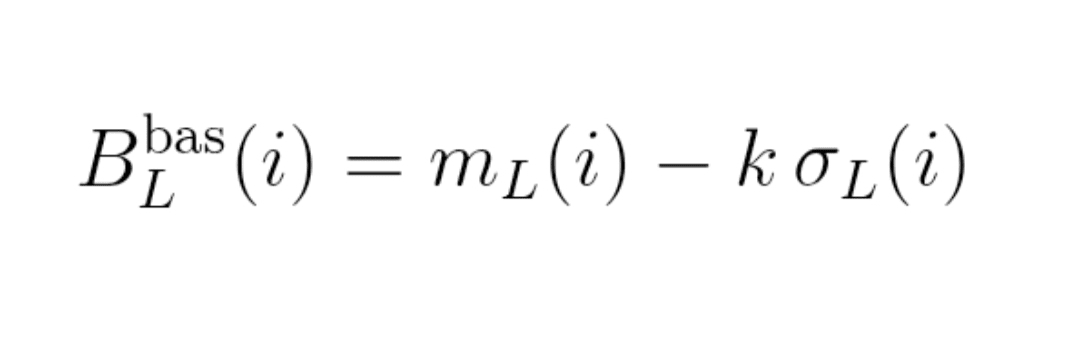
2.3. Normalisierter Preis im Tunnel
Wir schauen dann, wo der Preis in Anzahl der Sigmas liegt:
Formel (4) : normalisierter Preis
z_L(i) = (P_i − m_L(i)) / σ_L(i)
z_L(i) ≈ 0 : Preis in der Mitte des Tunnels,
|z_L(i)| ≈ 1, 2, 3 : Preis, der sich den Bändern nähert oder sie berührt.
Alles, was folgt, geschieht in diesem normalisierten Bezug z_L.
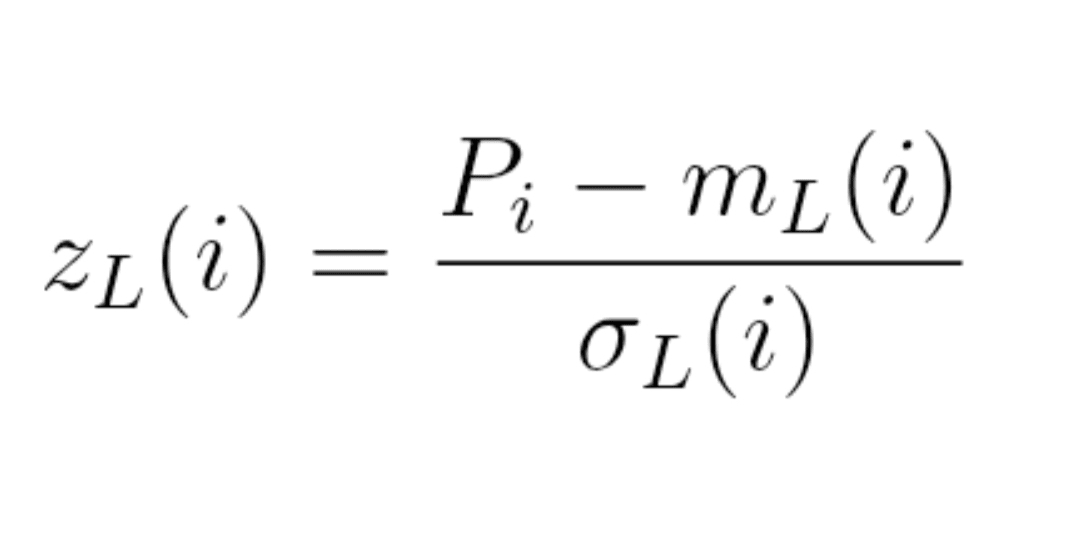
3. Messe die „Rauheit“ des Preises zwischen den Bändern
Intuition:
Tiefer Markt → der Preis gleitet eher sanft in seinem Tunnel.
Leerer Markt → der Preis ist nervös, gezackt, springt sehr schnell von einer Seite zur anderen des Tunnels.
Wir messen diese Rauheit mit einer diskreten Dirichlet-Energie.
Wir betrachten ein Fenster von Indizes von i_0 bis i_1.
Formel (5) : Energie E_L
E_L(i_0, i_1)
= 1/2 × Summe für i von i_0 bis i_1 − 1 von [ z_L(i+1) − z_L(i) ]²
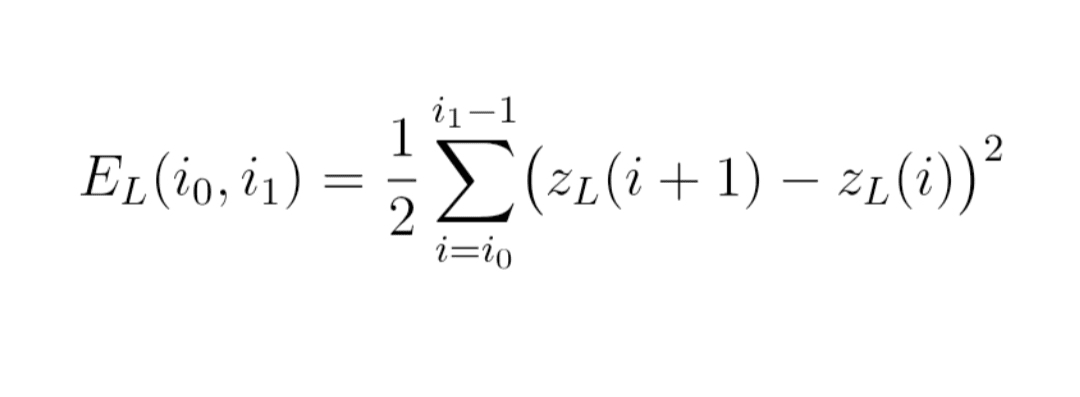
Dann normalisieren wir durch die Länge des Fensters, um eine Dichte zu erhalten:
Formel (6) : Energiedichte ε_L
ε_L(i_0, i_1) = E_L(i_0, i_1) / (i_1 − i_0)
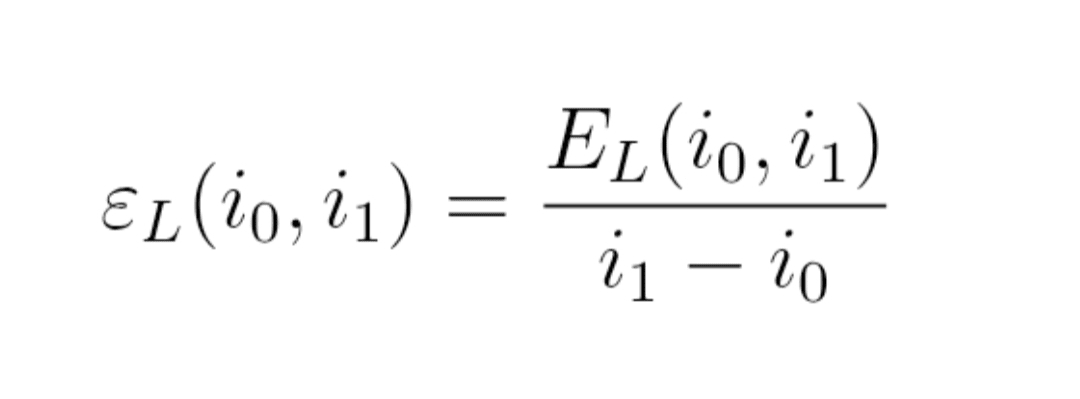
Lesen:
ε_L klein → z_L-Bahnen eher glatt,
ε_L groß → z_L-Bahnen sehr zackig.
Im Wesentlichen misst ε_L, wie stark der Preis innerhalb seines Bollinger-Bandes „zappelt“, unabhängig von der Preisskala (durch die Normalisierung mit σ_L).
4. Implizite Tiefe : ein einfacher Score Λ_L
Wir wollen jetzt diese Rauheit mit der Markttiefe verknüpfen.
4.1. Kleines stilisiertes Modell
Wir notieren:
Formel (7) : elementare Rendite
r_i = log(P_{i+1}) − log(P_i)
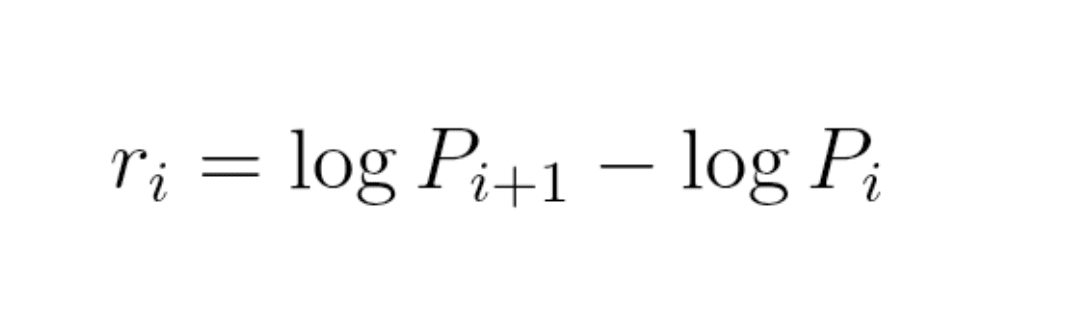
Wir nehmen ein sehr einfaches Modell an:
Formel (8) : mikroumstrukturmodell
r_i = (1 / Λ_i) × q_i + η_i
wo:
q_i = Ungleichgewicht der Orders (Marktkäufe − Marktverkäufe) im Intervall,
Λ_i = lokale Markttiefe,
η_i = „Geräusch“ (Nachrichten, fundamentale Ströme…).
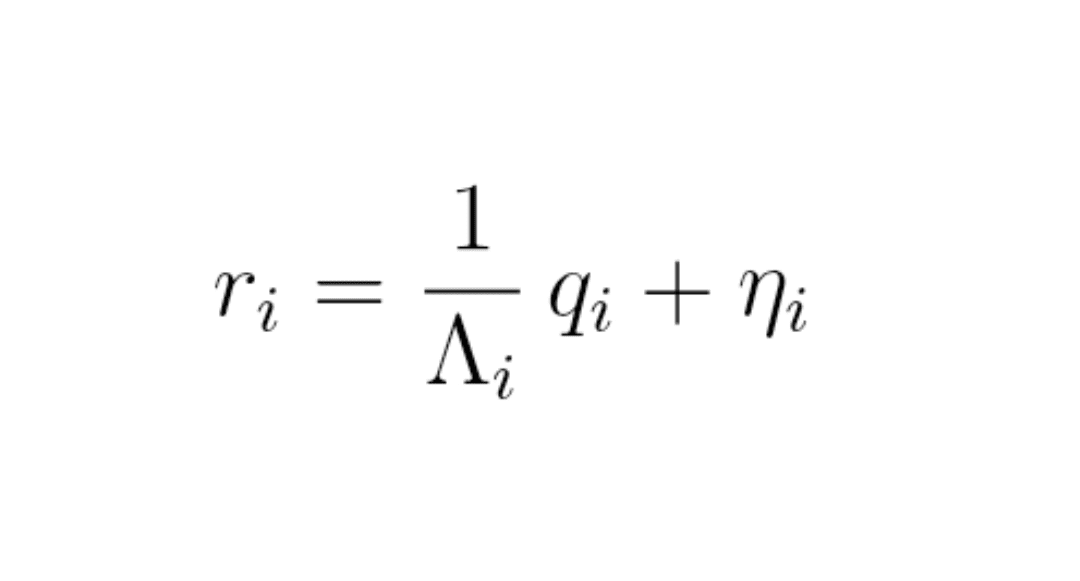
Ohne DOM sehen wir weder q_i noch Λ_i.
Aber wir sehen r_i, also z_L, also ε_L.
Indem wir über die Varianzen nachdenken und die Konstanten zusammenfassen, kommen wir zu einer Beziehung vom Typ:
Formel (9) : Varianz der Renditen (Schema)
E[r_i²] ≈ σ_q² / Λ² + σ_η²
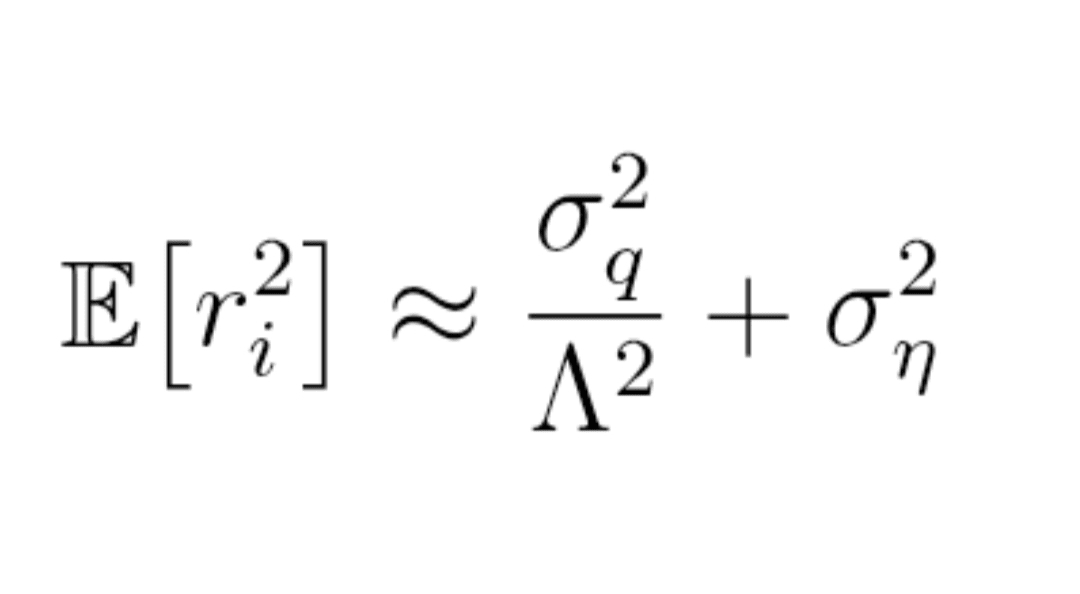
(im Durchschnitt über das Fenster, σ_q und σ_η sind Konstanten, Λ die typische Tiefe).
Der Schlüsselgedanke: Je kleiner Λ ist, desto größer ist der Term σ_q² / Λ², also desto größer ist r_i² → desto mehr wird der Preis für denselben Orderfluss bewegt.
Durch die Verknüpfung von z_L und r_i (z_L ist grob gesagt die Rendite geteilt durch σ_L), erhält man, dass ε_L steigt, wenn Λ abnimmt.
Daher ein sehr einfacher Score für die implizite Tiefe 👇
4.2. Praktische Definition des Scores Λ_L
Formel (10) : Score der impliziten Tiefe
Λ_L ≈ C_L × σ_L / Quadratwurzel von ε_L
wo:
σ_L = lokale Volatilität,
ε_L = Energiedichte,
C_L = Konstante, die auf einem Paar kalibriert werden muss, bei dem das DOM sichtbar ist.
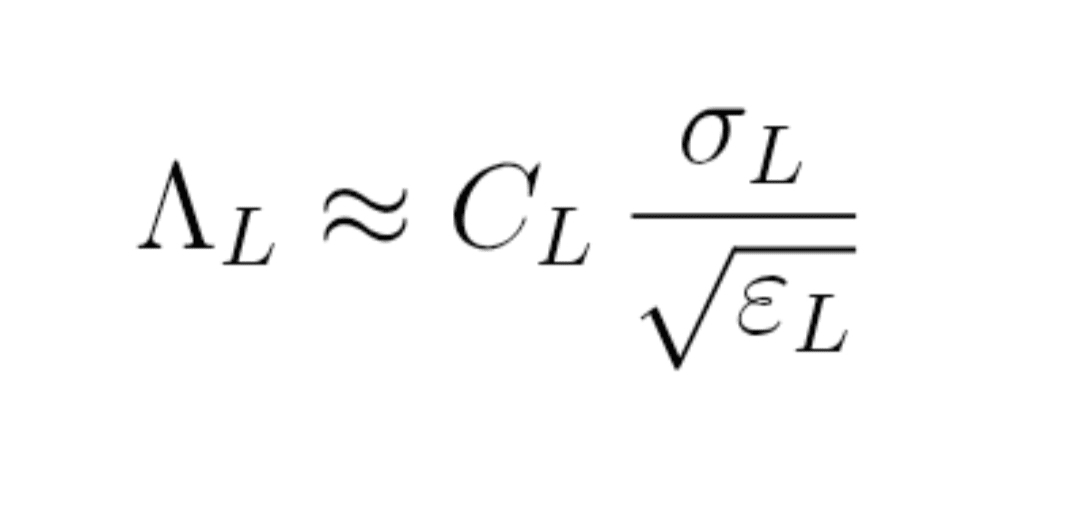
Lesen:
ε_L groß → der Markt absorbiert gut die Orderflüsse → starke Tiefe.
Λ_L klein → der Preis „ruckelt“ viel für dasselbe σ_L → leerer Markt.
Du hast jetzt einen Hinweis auf das implizite Volumen, ohne das Orderbuch zu sehen. 🤩
5. Implizites Volumen bis zu den Bändern
In vielen Mikroumstrukturmodellen ist das Volumen, das benötigt wird, um den Preis um ein bestimmtes Δp zu bewegen, proportional zu Λ_L × |Δp|.
Wenn man schaut, was bis zu den Bändern bei k Standardabweichungen passiert:
Δp = k × σ_L.
Wir können dann ein implizites Volumen bis zu den Bändern definieren:
Formel (11) : implizites Volumen V_L^imp
V_L^imp (Δp = k σ_L)
≈ k × C_L × σ_L² / Quadratwurzel von ε_L
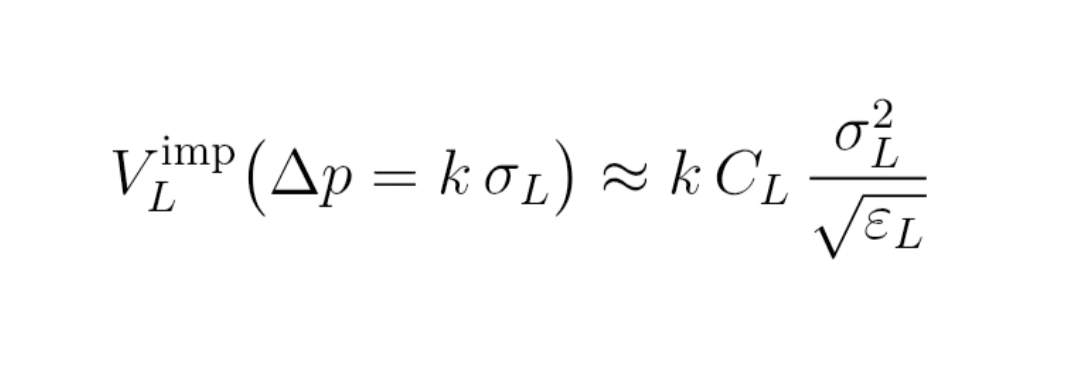
Dieses V_L^imp ist eine Größenordnung des Volumens, das (im Durchschnitt) benötigt wird, um das versteckte Orderbuch bis zu den Bollinger-Bändern zu fegen.
Auf einem Paar mit DOM kannst du vergleichen:
V_L^imp ↔ kumuliertes tatsächliches Volumen im Orderbuch.
Auf dem Alpha-Markt hast du nur V_L^imp… aber das ist schon ein Kompass. 🧭
6. Wie man das auf Binance anwendet
6.1. Phase 1 : Kalibrierung auf einem Paar mit sichtbarem DOM
1. Wähle ein sehr liquides Paar (BTCUSDT, ETHUSDT Spot).
2. Live:
holt sich die Preise (Trades oder 1s Kerzen),
holt sich DOM-Snapshots (kumulierte Tiefe bis ±0,1 %, ±0,5 %, ±1 %, usw.).
3. Für jedes Fenster:
berechne m_L, σ_L, ε_L,
berechne den Rohindikator S_L = σ_L² / Quadratwurzel von ε_L,
misst das kumulierte tatsächliche Volumen V_obs im DOM bis Δp = k σ_L.
4. Mache eine einfache Regression:
Formel (12) : empirischer Zusammenhang
V_obs ≈ C_L × S_L
(mit S_L = σ_L² / √ε_L)
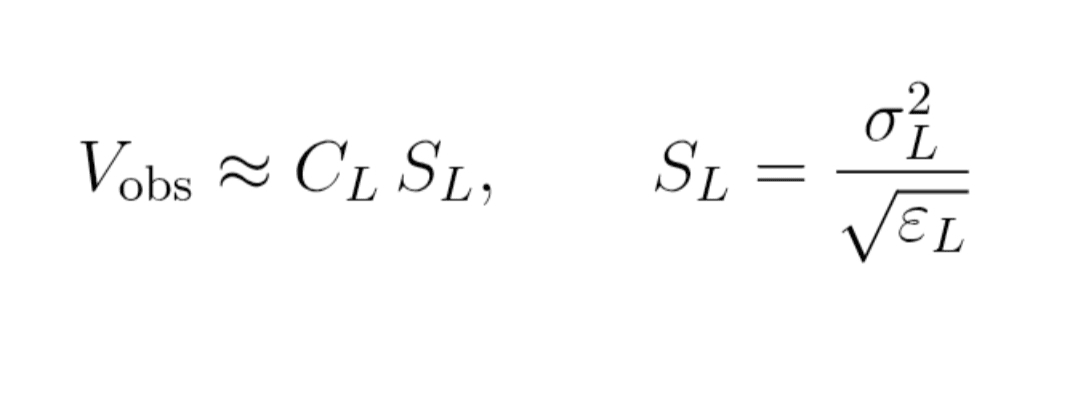
Du schließt die Konstante C_L für diese Skala L.
6.2. Phase 2 : Anwendung auf den Alpha-Markt (ohne DOM)
1. Auf deinem Alpha-Paar:
holt sich die Preise live,
berechne m_L, σ_L, ε_L.
2. Wende die Formel an:
Formel (13) : finales implizites Volumen
V_L^imp (Δp = k σ_L) ≈ k × C_L × σ_L² / √ε_L
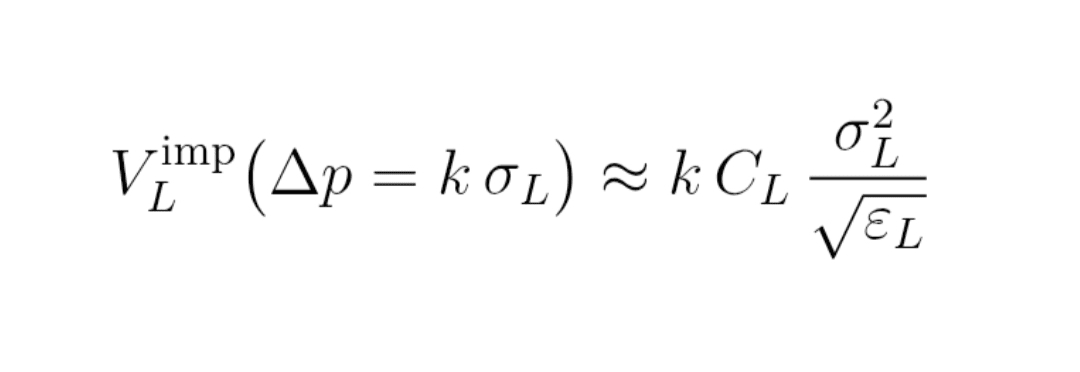
3. In Echtzeit anzeigen:
der Score Λ_L,
die Kurve Δp ↦ V_L^imp (dein Phantom-DOM).
7. Praktische Anwendung für deine Orders
7.1. Eine von Λ_L abhängige Treppe bauen
Wenn Λ_L hoch ist: tiefer Markt,
du kannst:
die Ebenen deiner geometrischen Progression näherbringen,
ordere Größen in ausreichendem Maße gleichmäßig halten.
Wenn Λ_L niedrig ist: leerer Markt,
du kannst:
die Ebenen weiter auseinanderziehen,
die Größe der Orders in der Nähe des Preises verringern,
halte Volumen für entferntere Ebenen.
7.2. Lese die impliziten „Liquiditätslücken“
Während man Λ_L in Echtzeit betrachtet:
Λ_L fällt abrupt, während σ_L sich nicht viel ändert:
Warnung: der Markt wird fragil,
du kannst den Hebel verringern, die Stops erweitern, das zu aggressive „Markt“ vermeiden.
Λ_L steigt nach einem Schock:
Zeichen der Resilienz: die Tiefe kommt zurück, der Markt zieht sich zusammen.
8. Grenzen und gesunder Menschenverstand
Das ist kein Orakel:
sieht die Spoofer nicht,
versteht keine makroökonomischen Nachrichten,
ersetzt nicht dein Money Management.
Der Indikator hängt ab von:
von der Wahl des Fensters N_L,
von der Qualität der Kalibrierung C_L,
der Granularität der Daten.
Zu verwenden als:
ein Radar für implizite Tiefe, als Ergänzung deiner technischen Analyse,
nicht als magischer „Kaufen/Verkaufen“-Knopf.
9. Um weiterzugehen
Dieser Artikel liefert die „Trader“-Version.
Dahinter steckt eine kleine Theorie:
Funktion z_L gesehen als Funktion auf einer Kette (Graph),
Dirichlet-Energie,
Verbindung mit der Wärmegleichung und der schrittweisen Glättung.
In einem separaten mathematischen Artikel können wir all dies ausführlich darlegen, mit Beweisen unterstützt auf dem TikTok-Konto @Maths4Traders 💪🤩

